Calibración y regresión

Socios en la medición

Por Khalid S. Al-Ghamdi

P.: ¿Cómo utilizamos el análisis de regresión para la calibración?

R.: Como término estadístico, regresión tuvo su origen en el artículo de 1866 de Sir Francis Galton (1822-1911) titulado “Regression towards mediocrity in hereditary stature” (Regresión hacia la medianía en estatura hereditaria). Originalmente, Galton utilizó la palabra reversión en vez de regresión. Galton estudió la relación entre las estaturas de los padres y las estaturas de sus hijos. Estudió las estaturas de 928 adultos nacidos de 205 parejas de padres. Consideró el promedio de las estaturas del padre y de la madre como la variable predictora  y las estaturas de sus respectivos descendientes como la variable dependiente . Descubrió que los padres excepcionalmente altos, es decir, más altos que el promedio (o medianía), tendían a tener hijos que eran más bajos que ellos, y los padres que eran más bajos que el promedio tendían a tener hijos más altos que ellos. Entonces, formuló su teoría de la “regresión a la medianía” para representar la tendencia en la relación entre las estaturas de los padres y de los hijos.

Existen dos tipos de relaciones: la funcional y la estadística. Una relación funcional puede expresarse como y = f(x), donde x es la variable independiente e  es la variable dependiente. Si se trazan los puntos de datos bivariados (x,y)  caerán exactamente en la curva descrita por y = f(x). Una relación estadística puede describirse como , donde el símbolo  representa un error aleatorio y las letras mayúsculas para X e Y indican que no son valores fijos sino variables aleatorias. Según el contexto, X puede considerarse como fija o aleatoria. Si se trazan los puntos de datos bivariados generados mediante la observación del proceso (X,Y), estos no caerán exactamente en la curva descrita por y = f(x). En esta relación, X se denomina variable independiente, regresor o variable explicativa; Y se conoce como la variable dependiente o variable de respuesta.

La terminología relacionada con la calidad y la estadística (E456) define la calibración como un “proceso para establecer una relación entre un dispositivo de medición y un valor o valores estándar conocidos”. La Organización Internacional de Normalización (ISO) define la calibración (VIM, JCGM 200:2012) como una “operación que, en condiciones especificadas, en un primer paso establece una relación entre los valores de cantidades con incertidumbres de medición proporcionados por los estándares de medición y las correspondientes indicaciones con incertidumbres de medición relacionadas, y en un segundo paso utiliza esta información a fin de establecer una relación para obtener un resultado de medición a partir de una indicación”. Entonces, en metrología, la calibración del dispositivo de medición “establece” o estima la relación entre las entradas conocidas y las salidas medidas y el error aleatorio o incertidumbre en las salidas medidas. Esto se logra a través del análisis de regresión. Siempre que hay una actividad de medición en proceso hay calibración detrás de ella, y la calibración se basa en la regresión, excepto en el caso de los instrumentos de lectura directa.

La forma más simple de regresión, y la forma más utilizada en la calibración, es la regresión lineal. La función general de regresión f(X) se reemplaza por una función lineal, que nos da . El error  se supone que tiene una media 0 y una varianza . Los parámetros a y b se estiman casi siempre utilizando mínimos cuadrados ordinarios (OLS). Esto se realiza encontrando los valores de a y b (indicados como  y ) que minimizan la suma de los residuos elevados al cuadrado,  

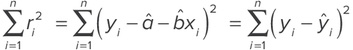
donde  es el valor promedio estimado de la respuesta y correspondiente al valor de. Los residuos son la diferencia entre los valores observados de y y los valores esperados de la ecuación de regresión. El parámetro b es la pendiente de la línea, y a es la intersección con el eje y.

En la calibración clásica, la variable independiente es el mensurando, la propiedad que se mide, representada por el conjunto de valores del estándar de calibración. La variable de respuesta es la lectura (indicación) del instrumento. El estimador de pendiente  es el coeficiente de sensibilidad, el cambio de la respuesta promedio ante un cambio unitario del mensurando. El parámetro  es un estimador de la lectura promedio cuando el valor del mensurando es cero, como para una muestra testigo.

Figura 1.

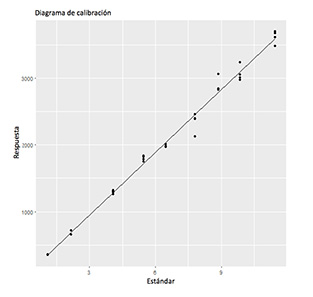
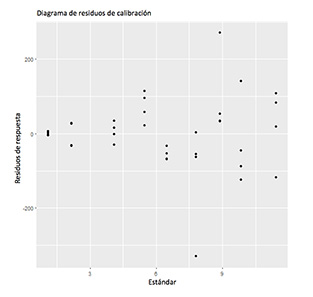
Los residuos deben distribuirse de forma aproximadamente normal con una dispersión constante. La figura 1 muestra un ejemplo de un diagrama de calibración. Sin embargo, la figura 2 indica que el patrón del diagrama de residuos en función de los valores ajustados muestra un aumento de la dispersión con un nivel creciente del estándar. No es raro que la dispersión de los residuos sea una función creciente del mensurando (y de los valores ajustados). En química analítica, la varianza de las mediciones repetidas sigue comúnmente una ley potencial. En estos casos, el análisis de mínimos cuadrados ordinarios (OLS) no es apropiado. El modelo de calibración debe ajustarse mediante el análisis de mínimos cuadrados ponderados (WLS) con pesos inversamente proporcionales a la varianza de la medición repetida para asegurar la mayor exactitud posible en los estimadores de los parámetros. La varianza de la medición repetida se puede estimar utilizando muchos elementos repetitivos en cada nivel del mensurando y calculando una varianza en cada nivel, o estimando una regresión (no lineal) para la varianza como una función del mensurando.

Figura 2.

La calibración inversa es la regresión que se realiza utilizando la lectura del instrumento como la variable explicativa y el valor estándar como la variable de respuesta. El valor de mensurando de un elemento de prueba desconocido se calcula entonces directamente a partir de la ecuación de calibración inversa en lugar de invertir la ecuación de calibración ordinaria. En el caso en que la indicación del instrumento es multivariada, como ocurre en muchas aplicaciones espectroscópicas, la calibración inversa es el único enfoque posible. En tales casos se realiza utilizando técnicas tales como la regresión lineal múltiple, la regresión de componentes principales (PCR) o el análisis de mínimos cuadrados parciales (PLS).

Un buen diseño de calibración es esencial para construir un buen modelo de calibración. Los niveles estándar deben cubrir el rango de medición previsto. A menudo se recomiendan de 4 a 7 niveles para que el ajuste del modelo se pueda verificar mejor en el rango de trabajo, de modo que se pueda comprobar la constancia de la varianza y dar mejores estimadores de parámetros. A veces se usan modelos cuadráticos o no lineales en vez de los modelos lineales. Tener suficientes niveles estándar facilita la selección del modelo más apropiado utilizando el Análisis de varianza (ANOVA). Debe haber suficientes elementos repetitivos en cada nivel (de 3 a 7) para estimar la varianza de la respuesta.

La frecuencia de la calibración no debe ser mayor que la requerida, para evitar un ajuste excesivo del sistema de medición y para reducir los costos de calibración asociados. La calibración se puede monitorizar midiendo periódicamente un estándar de calibración elegido y generando un diagrama de control del resultado. Una señal en el diagrama de control indica la necesidad de una recalibración. Esta es una calibración basada en la condición, aunque también debe usarse un intervalo de tiempo máximo para la recalibración a fin de cumplir los requisitos de ISO/IEC 17025.

La calibración se usa universalmente en la ciencia de la medición. La regresión es la técnica más poderosa y más ampliamente utilizada en estadística. Es apropiado que las dos funcionen juntas de la mejor manera.