Standardization News:

P: ¿Qué tan bueno es mi modelo de regresión lineal?

R: La práctica para el análisis de regresión con una sola variable de predicción (E3080) fue revisada en 2019 para dar énfasis a la aplicación práctica de la regresión lineal simple. Ahora, guía al usuario a través del procedimiento para realizar un análisis de regresión lineal entre dos variables numéricas a fines de predecir una variable a partir de la otra, enfocándose más en el modelo, la estimación de los parámetros del modelo, la evaluación del modelo y los métodos para predecir un valor medio o un valor futuro.

Un paso fundamental para llevar a cabo un análisis de regresión es la evaluación del modelo, en particular la relevancia de la variable de predicción, el grado de cumplimiento de los supuestos de análisis subyacentes y la medida en que la variable de predicción explica la variación de la respuesta. Si no se evalúa, cualquier predicción basada en el modelo o en el conocimiento de los procesos o controles potenciales puede ser engañosa.

A continuación se presentan algunos métodos sencillos de diagnóstico de modelos gráficos y computacionales descritos en la práctica E3080 que suelen utilizarse para evaluar un modelo de regresión lineal simple. Algunos de estos métodos pueden ampliarse a modelos de regresión lineal con más de una variable de predicción.

En primer lugar, veamos el modelo de regresión lineal simple y los supuestos subyacentes.

Un modelo de regresión lineal simple toma la forma de la función de regresión rectilínea Y = β₀ + β₁X donde X es la variable de predicción; Y es la variable de respuesta; β₀ es la intersección, que representa el valor de Y cuando X = 0; y β₁ es la pendiente, que representa el cambio en Y para un cambio de una unidad en X. Dado un conjunto de pares de valores (X, Y), E3080 describe cómo calcular la pendiente y la intersección.

Sin embargo, no basta con hacer estos cálculos. Para que el modelo sea útil, debe existir una relación. Es decir, la pendiente debe ser lo suficientemente diferente de 0 como para decir que X es un predictor estadísticamente relevante de Y. Aunque esto no infiere directamente una relación causa-efecto entre las dos variables, sí indica que X explica cierta parte de la variación observada en Y.

Un método descrito en E3080 para evaluar qué tan diferente es la pendiente con respecto a 0 es construir un intervalo de confianza del 95 % alrededor del valor estimado de la pendiente. Si el intervalo de confianza no contiene 0, entonces X se considera un predictor estadísticamente relevante de Y.

La evaluación de la relevancia de la variable de predicción es un paso fundamental para establecer un modelo de predicción. Otro paso es verificar que el modelo representa adecuadamente la relación entre X e Y. Si se traza y compara con los datos, el modelo debe encajar a la mitad de los datos con los valores de respuesta observados aleatoriamente por encima o por debajo del modelo. Esta variación representa un error aleatorio. Para cada valor de respuesta observado Y, se puede calcular un valor de error como el valor observado menos el valor predicho basado en el modelo. Usualmente, este valor se denomina residuo.

La colección de valores residuales se utiliza para evaluar los supuestos subyacentes en la regresión lineal simple: 1) la distribución de los residuos se distribuye normalmente con media 0 y varianza constante s²; 2) los residuos son independientes; y 3) la relación es una función de regresión rectilínea. En la figura 1 se muestra una representación gráfica de estos supuestos.

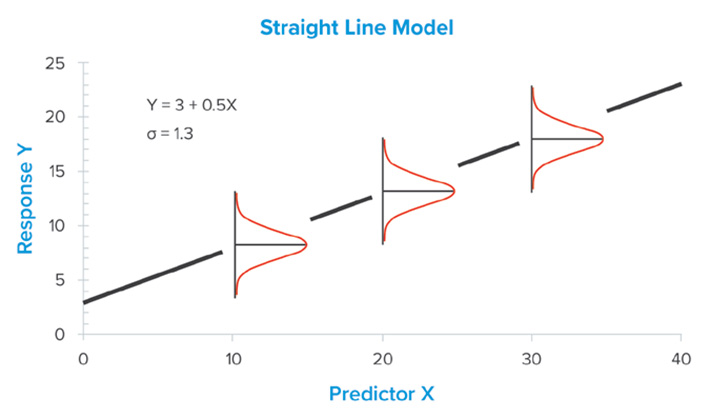
Figura 1: Este gráfico ilustra los supuestos subyacentes en el análisis de regresión lineal simple. Aparece como Fig. 2 en E3080.

Un gráfico de los residuos frente a sus valores X, conocido como gráfico de residuos, se utiliza para evaluar los supuestos de linealidad, varianza constante e independencia.

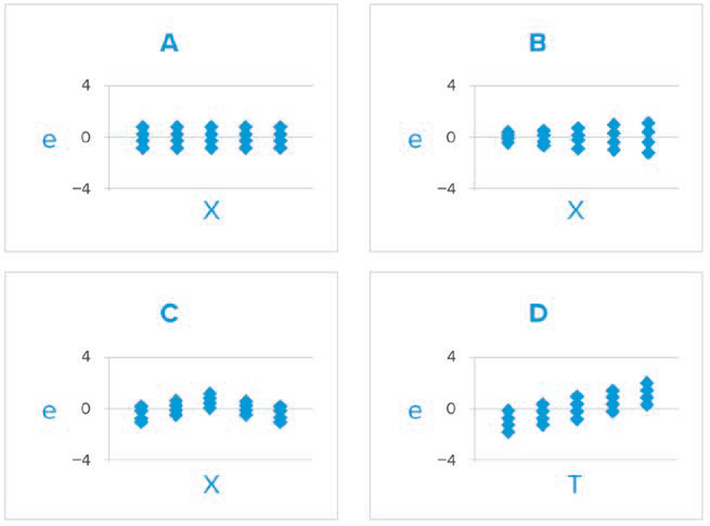
La figura 2 muestra cuatro ejemplos de gráficos de residuos, donde e indica el residuo.

El gráfico A muestra el patrón deseado de variación aleatoria alrededor de 0 en el rango de valores de X que indica que las suposiciones de linealidad y varianza constante se mantienen. Si el modelo pasa directamente por el centro de la relación y la variación alrededor del modelo es constante en el rango de valores X, los residuos deberían variar aleatoriamente alrededor de 0 dentro de un rango dado cuando se grafican contra sus valores X. En otras palabras, el patrón en el gráfico de residuos imitará la forma en que el modelo se ajusta a los datos. Si, por ejemplo, a medida que X aumenta, los valores observados se encuentran por debajo del modelo, luego por encima, luego por debajo, el gráfico de residuos mostrará un patrón de "arco iris" como en el gráfico C, lo que indicaría que el supuesto de linealidad no se cumple. En algunos casos, el supuesto de linealidad puede mantenerse, pero la variación alrededor del modelo no es constante. El gráfico B muestra una variación creciente a medida que aumenta X. Aunque la presencia de una varianza no constante puede ser relevante en la práctica o no, no debería ignorarse, ya que puede dar lugar a estimaciones de intervalo engañosas para los valores predichos, ya que las fórmulas de intervalos estadísticos asumen una varianza constante. Si el orden de la prueba está disponible y un gráfico de los residuos contra el orden de la prueba muestra un patrón como el del gráfico D, entonces no se cumple la suposición de residuos independientes. Un gráfico de residuos también sirve como herramienta visual para detectar valores atípicos, que también pueden afectar negativamente al modelo.

Figura 2: Este gráfico muestra ejemplos de patrones que pueden observarse en los gráficos de residuos. Aparece como Figura 3 en E3080.

La suposición de una distribución normal de residuos centrada en 0 puede evaluarse visualmente con un histograma. Si se mantiene la hipótesis de normalidad, el histograma debería tener una forma aproximada de campana y ser simétrico respecto de 0.

Si alguno de los supuestos de regresión subyacentes no se cumple o si hay valores atípicos importantes, el modelo puede no ser adecuado. Sin embargo, no todo está perdido. La práctica E3080 incluye un análisis de las posibles medidas correctivas. Por lo tanto, el análisis de regresión puede ser un proceso iterativo para asegurar que se cumplan todos los supuestos del modelo subyacente.

El último paso en la evaluación de la idoneidad del modelo consiste en evaluar en qué medida la variable de predicción relevante X explica la variación observada en Y. Para una regresión lineal simple, esto se evalúa observando el coeficiente de determinación. Denominado r², este valor es el cuadrado del coeficiente de correlación, r, y normalmente se expresa en porcentaje. Un valor cercano a 100 % significa que X explica casi toda la variación de Y. Un valor bajo puede indicar que puede haber otras variables además de (o en lugar de) X que pueden ayudar o explicar mejor la variación en Y. Si la variable de predicción no es relevante, con frecuencia esto se reflejará en un valor cercano a 0. Si los supuestos de regresión subyacentes no se cumplen, la interpretación de r² carece de sentido.

En resumen, el modelo resultante de un análisis de regresión lineal simple se considera "bueno" y es de uso práctico relevante, solamente si:

• la variable de predicción es relevante,
• se cumplen los supuestos subyacentes del modelo, y
• la variable de predicción explica un gran porcentaje de la variación observada en la respuesta.

Dado que existen programas comerciales de software fácilmente disponibles para realizar los cálculos necesarios, el énfasis principal debe ponerse en la evaluación del modelo para garantizar que se produzca un modelo de calidad.

Jennifer Brown trabajó como estadística en la industria aeroespacial durante más de 12 años y ahora es consultora estadística independiente. Es miembro del comité de calidad y estadística (E11) y presidenta de su subcomité de terminología (E11.70). También es miembro del subcomité de métodos especializados de ensayos no destructivos (E07.10) y es el contacto técnico para dos de sus estándares relacionados con datos.

El Dr. John Carson, estadístico sénior de Neptune and Co., es el coordinador de la columna Data Points. Es miembro del comité de calidad y estadística (E11) y miembro de los comités de productos a base de petróleo, combustibles líquidos y lubricantes (D02), calidad del aire (D22) y evaluación ambiental, gestión de riesgos y acción correctiva (E50).