Standardization News:

P: ¿Qué es la varianza no constante y por qué es una preocupación cuando se ajusta el modelo?

R: Uno de los supuestos en los que se basa la regresión lineal es el de la varianza constante. Pero, ¿qué significa esto exactamente, cuándo puede incumplirse, por qué es importante comprobar la varianza constante y si puede considerarse en un análisis de regresión lineal?

Un modelo de regresión lineal incluye dos submodelos importantes: 1) el modelo que relaciona el valor esperado de la variable de respuesta, Y, con una o más variables predictoras independientes, y 2) el modelo que describe la varianza de Y para un valor dado de la variable predictora. Consideremos el modelo teórico de regresión lineal simple Y = β0 +β1X + ε. El submodelo (1) es β0 +β1X, que relaciona Y con la única variable predictora, X, a través de una función lineal. El submodelo (2) ε, a menudo denominado término de error, modela la varianza de Y para un valor dado de X y se supone que se distribuye normalmente con una media de 0 y una varianza constante de σ2 en un análisis de regresión lineal.

El submodelo (2) se relaciona con los datos y el modelo ajustado de la siguiente manera. Digamos que el modelo ajustado está representado por Y ^_i=b_0+b_1 X_i, donde Y_i es el i-ésimo valor observado con un valor de variable predictora de X_i, b_0 es el valor estimado de la intersección del modelo, b_1 es el valor estimado de la pendiente del modelo, y Y ^_i es el valor predicho para Y_i basado en el modelo. Como se ilustra en la Figura 1 [haciendo referencia a la práctica estándar para el análisis de regresión con una sola variable predictora (E3080)], la varianza en Y para un valor dado de X se supone que sigue una distribución normal con una dispersión que permanece constante a diferentes valores de X, pero con un centro cerca del valor predicho Y ^=b_0+b_1 X. En otras palabras, el centro del error, con una distribución normal alrededor del modelo, cambia a medida que cambia el valor de X, pero la dispersión de Y se mantiene igual en diferentes valores de X.

Aunque no aparece ningún término de error en el modelo ajustado, se puede calcular un valor de error, a menudo denominado valor residual, para cada valor observado como la diferencia entre el valor observado y el valor predicho en función del modelo, o e_i=Y_i-(Y_i ) ^ . La recopilación de valores residuales se utiliza para estimar la varianza de Y en un valor X dado. Es decir, σ ^^2=(∑_(i = 1)^n▒e_i^2 )⁄((n-1) ). La raíz cuadrada del valor σ ^^2 se utiliza para estimar el valor de la desviación estándar constante, σ ^.

 
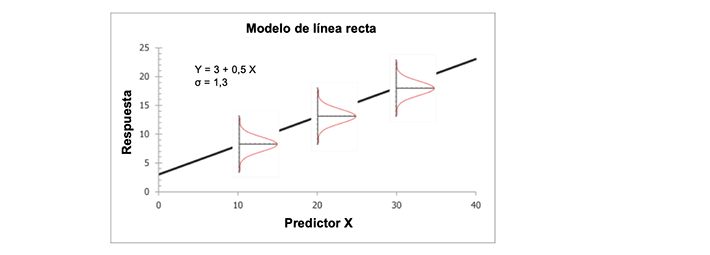
Figura 1. Ilustración del supuesto de normalidad y varianza constante en el análisis de regresión lineal, que aparece como Figura 2 en E3080.

En la Figura 2, se muestran ejemplos de varianza constante y no constante en valores Y observados para valores dados de una variable predictora, X. Los gráficos A y B muestran observaciones tomadas en valores discretos de X, que, por ejemplo, pueden ilustrar datos recogidos de un experimento planificado. Los valores Y en el gráfico A muestran una varianza constante a medida que X aumenta, mientras que los valores Y en el gráfico B muestran una variación creciente a medida que X aumenta. El gráfico C muestra datos para Y en un rango de valores para X, que, por ejemplo, pueden ilustrar datos observacionales. Los valores observados para Y en el gráfico C muestran una varianza creciente a medida que X aumenta. (Tenga en cuenta que, en algunos casos, los valores observados en Y pueden exhibir una varianza decreciente a medida que X aumenta).

Hay muchas situaciones en las que se espera que la varianza en Y sea constante en todo el rango de valores de X. Por ejemplo, los valores de Y en el gráfico A pueden representar datos experimentales recopilados en un dispositivo de medición que se espera tenga un error constante (es decir, una varianza constante) o un error casi constante dentro del rango de la capacidad de medición del instrumento (valores X), a menudo denominado “rango de trabajo”. También hay situaciones en las que no se espera que la varianza sea constante. Los valores Y en el gráfico B, por ejemplo, pueden representar longitudes medidas de pernos fabricados a varias longitudes nominales (X), donde se puede esperar que los pernos con una mayor longitud nominal tengan una mayor varianza en su longitud final fabricada (Y) en comparación con los pernos con una longitud nominal más corta.

A veces, la varianza no constante es obvia en los datos y, a veces, es sutil. Las pruebas estadísticas formales para la varianza no constante están disponibles y, generalmente, se recomiendan cuando se realiza un análisis de regresión lineal. Si se espera que la variación sea constante, pero los datos o las pruebas estadísticas formales sugieren lo contrario, esto puede indicar que hay otra variable que influye en el proceso y que debe tenerse en cuenta.

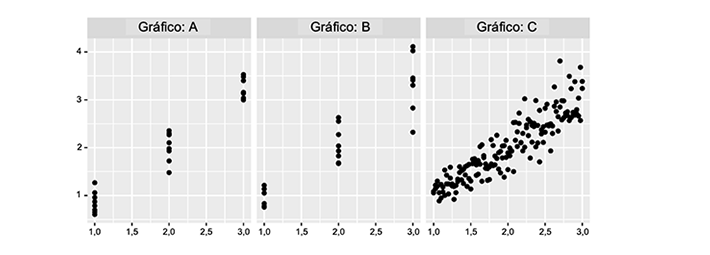
Figura 2. En el gráfico A, se ilustra la varianza constante. En los gráficos B y C, se ilustra la varianza no constante.

Es importante no pasar por alto el supuesto de varianza constante, ya que la presencia de varianza no constante puede tener un gran impacto en las estimaciones de varianza y, en consecuencia, en cualquier inferencia realizada utilizando intervalos de confianza o intervalos de predicción. La suposición de una varianza constante da como resultado límites de confianza y límites de predicción de forma hiperbólica, que son aproximadamente paralelos al modelo, pero se amplían un poco a medida que la distancia desde el centro de datos (¯X,¯Y)aumenta [E3080]. Si la variación en Y aumenta (o disminuye) a medida que aumenta el valor de X, los límites no reflejarán esto y se harán inferencias erróneas. En la Figura 3, se muestran los límites de predicción alrededor de dos modelos de los mismos datos, uno resultante de un análisis de regresión lineal que explica la varianza no constante (líneas continuas que muestran la forma de megáfono) y el otro resultante de un análisis de regresión lineal que ignora la varianza no constante observada en los datos (líneas discontinuas aproximadamente paralelas al modelo). Cualquier inferencia realizada que aplique los límites de predicción de varianza constante para valores mayores o menores de X, en este caso, será muy inexacta. Por lo tanto, si la varianza no constante está presente, debe tenerse en cuenta.

En el E3080, se analizan algunos de los métodos comunes utilizados en el análisis de regresión lineal para considerar la varianza no constante, como la transformación de variables. Los métodos alternativos, como la regresión ponderada de mínimos cuadrados, también pueden servir como medida correctiva. Además de la varianza constante, hay otros supuestos importantes en el análisis de regresión lineal que deben verificarse.

Se alienta al lector a consultar la práctica E3080 para obtener información sobre todos los supuestos subyacentes, los métodos prácticos para verificar la validez de los supuestos y las medidas correctivas que deben aplicarse si se incumplen uno o más supuestos.

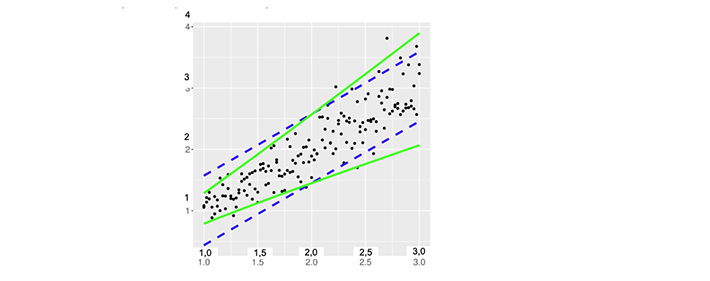
Figura 3. Ilustración de un intervalo de predicción resultante de un análisis de regresión lineal que explica la varianza no constante (líneas continuas que muestran la forma de megáfono) y uno resultante de un análisis de regresión lineal que ignora la varianza no constante (líneas discontinuas aproximadamente paralelas al modelo).

La Dra. Katie Daisey es una científica en Arkema Inc. dedicada al apoyo de I+D y fabricación en las áreas de estadística, quimiometría y transformación digital. La Dra. Daisey actualmente se desempeña como presidenta del comité de Calidad y estadísticas (E11).

Jennifer Brown es estadística y tiene 17 años de experiencia en la industria aeroespacial. Preside el subcomité de terminología (E11.70) y es miembro del subcomité de métodos especializados de ensayos no destructivos (E07.10).

El Dr. John Carson es estadístico senior de Neptune and Co. y coordinador de la columna Data Points. Es miembro de los comités de Calidad y estadísticas (E11), Productos derivados del petróleo, combustibles líquidos y lubricantes (D02), Calidad del aire (D22) y otros.