El modelo Weibull: reforzando el concepto de confiabilidad

Por Stephen N. Luko y Dean V. Neubauer

P. ¿Cuál es la distribución de Weibull y cómo se utiliza en el análisis de datos?

En una columna anterior de Data Points (número de ene./feb. de 2018), introdujimos los conceptos fundamentales de la confiabilidad. En esta entrega reforzamos el concepto de confiabilidad introduciendo la distribución de Weibull y su uso en el análisis de datos.

La distribución de Weibull es apropiada para muchos tipos de propiedades de materiales, así como para la vida útil de los componentes bajo una amplia variedad de condiciones, incluyendo escenarios de prueba y aspectos de campo. Puede modelar las tasas de fallas para las tres principales clasificaciones de modos de falla: mortalidad precoz o falla temprana, falla aleatoria y falla por desgaste.

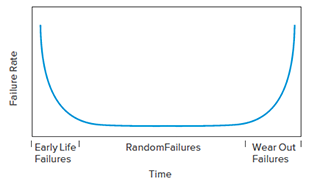
Figura 1. Curva de la bañera

En la figura 1 se muestra una tasa idealizada de fallas en el ciclo de vida conocida como curva de la bañera; en la figura se muestran las tres principales regiones del modo de falla y cómo funciona cada tasa de fallas en dichas regiones. La falla temprana generalmente significa que existe un modo de falla y que algunas unidades tienen la condición de falla más grave que otras, lo que las lleva a tener una mayor propensión a fallar de forma temprana, como un defecto de fabricación en un neumático.

A medida que se eliminan las fallas y se realizan mejoras, la tasa de fallas disminuye con el tiempo en este período. Con el tiempo, la tasa de fallas se estabiliza y se vuelve constante para cierto período de la vida útil. En este período, las fallas se producen de forma aleatoria y suelen deberse a condiciones externas, como el hecho de que un neumático pase por encima de un clavo y se desinfle o porque algún otro objeto extraño cause daños durante el uso.

Conforme pasa el tiempo, los productos tienden a perder robustez a medida que envejecen y se desgastan. Esto tiene como resultado una etapa en la vida del producto caracterizada por un aumento en la tasa de fallas, como cuando un neumático falla a causa de funcionar con un desgaste excesivo en la banda de rodamiento.

Es fácil trabajar con la distribución de Weibull, que tiene una función de distribución acumulativa de forma cerrada, F(t), como se muestra en la ecuación ¹. Esta se usa para modelar variables en el dominio [0,∞] y se lee como “el tiempo t no puede ser menor de 0 pero tiene un extremo abierto a la derecha porque no sabemos cuándo fallará”. La confiabilidad se calcula como se muestra en la ecuación ².

1)

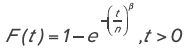
2)

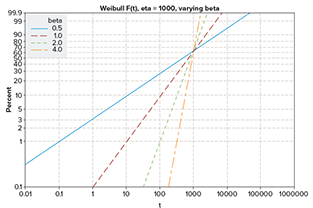
Figura 2. La función de distribución acumulativa de Weibull F(t), linealizada

En la ecuación 1, F(t) representa la probabilidad acumulada de que una unidad falle en el tiempo t; la cantidad 1-F(t) es la probabilidad de supervivencia, o confiabilidad en el tiempo t, llamada R(t) en (2). La distribución de Weibull tiene dos parámetros, η y β. El parámetro β, también llamado pendiente de Weibull, es adimensional y positivo, y normalmente se conoce como parámetro de forma porque, para diferentes valores de β y un valor de η fijo, F(t) tendrá una forma diferente.

Por ejemplo, cuando β = 1, la distribución de Weibull se convierte en distribución exponencial, y para β de entre 3 y 4, la distribución de Weibull se asemeja a una distribución normal. Los ingenieros también utilizan el término “pendiente de Weibull” porque la F(t) de Weibull puede ser linealizada y β es la pendiente de la línea resultante. β también caracteriza la dispersión en los resultados finales de la prueba. Los valores más altos de β generalmente significan menos dispersión. El parámetro η se llama parámetro de escala y tiene las mismas unidades que la variable t. Resulta que F(η) = 0,632 para cualquier β y que, por esa razón, también se utiliza el nombre vida característica para η.

La distribución de Weibull puede ser linealizada con unas pocas y simples operaciones algebraicas. Resulta la siguiente ecuación:

3)

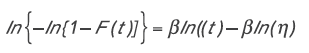
Observe cómo un valor mayor de β (pendiente) da lugar a una menor variación o dispersión. En un análisis típico de Weibull, hay datos en forma de fallas y probables pruebas interrumpidas antes de la falla (suspensiones u observaciones censuradas). Los datos se utilizan con uno de los procedimientos de estimación bien conocidos para estimar los parámetros η y β. Una vez completados, los resultados (fallas y modelo estimado) pueden ser representados gráficamente usando la técnica de trazado de probabilidad de Weibull. Esto se hace comúnmente usando cualquiera de los diferentes paquetes de software ampliamente disponibles. En este ejemplo, usamos la versión 19 de Minitab. El modelo resultante se utiliza luego con diversos fines, como los cálculos de confiabilidad o el pronóstico de fallas. El siguiente ejemplo resume el método.

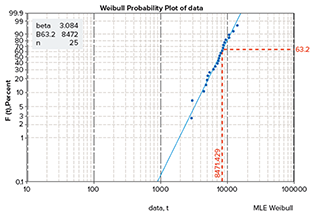
Figura 3. Gráfica de probabilidad de Weibull de los datos de los componentes aeroespaciales

En este ejemplo se utilizó n = 25 fallas que habían ocurrido en el campo para cierto tipo de dispositivo mecánico utilizado en la industria aeroespacial. Este era un diseño nuevo/mejorado que se estaba probando en el campo. La figura 2 muestra la gráfica de probabilidad resultante. El análisis produjo valores estimados de 3084 para beta (β) y de 8472 para la vida característica (η). Las unidades aquí son ciclos operativos. La probabilidad de falla en el tiempo t puede leerse directamente del gráfico, o podemos utilizar la función de distribución de Weibull (ecuación 1) con los parámetros estimados en varios valores de t. En la tabla 1 se muestra un ejemplo de esto. Esta tabla se puede generar fácilmente en Excel, donde F(t) = 1-EXP(-1*(t/ β)^β) y los valores de η y β están referidos a la ubicación de sus celdas. Observe que cuando F(t) = 63,2 %, se estima una vida característica η ≈ 8472. Además, con una estimación de β de 3 sabemos que el mecanismo de falla se debe al desgaste.

Tabla 1. Datos de campo para la distribución de Weibull: probabilidad de falla, F(t) y confiabilidad, R(t)=1-F(t), estimados

No se trata de una cuestión de seguridad, y el fabricante ha acordado un tiempo de garantía de 1500 horas. Los valores de la tabla muestran una confiabilidad estimada a t = 1500 ciclos de alrededor de 99,5 %, lo que da la seguridad de este valor al fabricante y al cliente. Se observa aquí que se están utilizando estimaciones puntuales de los parámetros de Weibull y los valores de confiabilidad asociados. Estos pueden considerarse como valores promedio aproximados. Si se consideran conjuntos de datos adicionales del mismo producto y condiciones de funcionamiento, esperaríamos valores como éstos, aunque pueden variar (hacia arriba o hacia abajo) un poco.
Se recomienda a los lectores interesados en obtener más detalles sobre la confiabilidad que consulten la guía de confiabilidad general (E3159) del comité sobre calidad y estadística (E11). Para obtener detalles del análisis, incluidos los errores resultantes del muestreo, consulte las referencias 3 o 4. Si está interesado en el uso de distribuciones de confiabilidad con fines de muestreo para aceptación, estos dos estándares tienen más información: el método sobre factores y procedimientos para aplicar los planes MIL-STD-105 en la inspección de vida útil y confiabilidad (E2555) y el método para pruebas de vida y confiabilidad basadas en la distribución exponencial (E2696).

Referencias

1. Luko, S.N., “What is Reliability–Key Concepts and Terminology” (Qué es la confiabilidad: conceptos clave y terminología) Standardization News, enero/febrero de 2018, pág. 28.

2. McCook, J.I., Using the Weibull Distribution, Reliability, Modeling and Inference (Uso de la distribución, confiabilidad, modelado e inferencia de Weibull). Wiley Series in Probability and Statistics (Serie Wiley sobre Probabilidad y Estadística), Hoboken, N.J., 2012.

3. Nelson, W., Applied Life Data Analysis (Análisis aplicado de datos de vida útil), John Wiley & Sons, Nueva York, N.Y., 1982.

Stephen N. Luko es miembro y estadístico de United Technologies Corp/Collins Aerospace. Es presidente del subcomité sobre confiabilidad, integrante del comité sobre calidad y estadística (E11), miembro de ASTM International, ganador del premio Harold F. Dodge y expresidente del Comité E11.

Dean V. Neubauer, coordinador de la columna Data Points, es ingeniero y jefe de estadística en Corning Inc. Es miembro general del subcomité ejecutivo del comité sobre calidad y estadística (E11), miembro de ASTM International y expresidente del comité E11.