Establecimiento de un límite superior de confianza en la proporción de no conformidad

Por Joel Dobson

P: ¿Es posible calcular un límite superior de confianza del 95 % para la proporción de no conformidad de las unidades restantes no inspeccionadas en un lote de N unidades, de las cuales tomamos una muestra de tamaño n para encontrar x unidades no conformes?

R: Comencemos con un ejemplo para explicar el método y los cálculos que dan las ecuaciones generales.

Supongamos que nuestro lote contiene N = 1000 unidades. Entre una muestra elegida al azar de n = 100, encontramos x = 1 unidad mala. Para el resto N - n = 900 unidades, estimamos que el 1 % será no conforme, lo cual es 9; pero podemos decir más que eso. En particular, nos sentimos un 95 % confiados en que no más del 4,656 % de ellas serán no conformes, lo cual es alrededor de 42 unidades.

¿Cómo llegamos a este porcentaje y número?

Para ilustrar el pensamiento detrás del método que sigue, intentemos primero adivinar el valor más pequeño del parámetro, p, de una distribución binomial con una muestra de n = 100, lo que nos da: {la probabilidad de que X sea menor o igual que uno} es menor que 0,05 o, simbólicamente, 'Prob (X < 1) < 0,05.’ Aquí, la variable X es el conteo de unidades malas observadas en nuestra muestra.

Sospechamos que este valor de p debería ser más grande que el 1 % no conforme observado porque deseamos que Prob (X < 1) < 0,05. De manera alternativa, esto es lo mismo que decir que deseamos que Prob (X > 1) > 0,95, o Prob (X > 2) > 0,95. ¿Cuál es el valor más pequeño de p que alcanza este objetivo? Como nuestra primera suposición, probemos un valor de p = 0,02. La función de densidad de probabilidad, o pdf, de un binomio tiene esta ecuación:

Donde X varía entre los números enteros de 0 a n. En nuestro ejemplo, tenemos:

O

Los primeros X dan valores de función de:

f(0) = 100!/(0! (100-0)!)*0,02^0*0,98^100 = 1 * 0,02^0 * 0,98^100 = 0,132620,
f(1) = 100! /(1! (100-1)!)*0,02^1*0,98^99 = 100 * 0,02^1 * 0,98^99 = 0,270652,
f(2) = 100! /(2! (100-2)!)*0,02^2*0,98^98 = (100*99/2) * 0,02^2 * 0,98^98 = 0,273414,
f(3) = 100!/(3! (100-3)!)*0,02^3*0,98^97 = (100*99*98/6) * 0,02^3 * 0,98^97 = 0,182276,

y así sucesivamente. Para cuando lleguemos a x = 12, el valor de esta función pdf será cercano a cero.

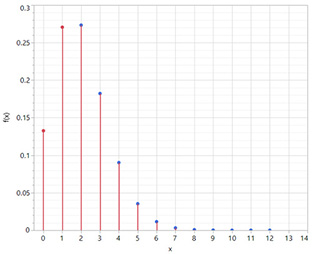
Podemos calcular estos valores en Excel usando ecuaciones como "=binomdist(0, 100, 0,02, 0)", "=binomdist(1, 100, 0,02, 0)", "=binomdist(2, 100, 0,02, 0)", etc. La probabilidad de ver 1 o menos es de 0,403272. Podemos obtener esto en Excel usando "=binomdist(1, 100, 0,02, 1)". La probabilidad de ver 2 o más es de 1 - 0,403272 = 0,596728, o alrededor del 60 %. Un gráfico de la función de densidad de probabilidad (pdf) se ve así (para los primeros 13 términos).

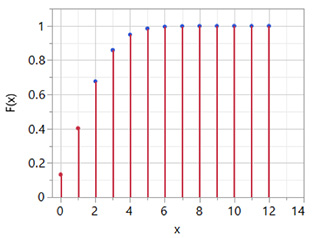
Un gráfico de la función de distribución acumulada (cdf) se ve así (para los primeros 13 términos).

La función de distribución acumulada (cdf) de x = 1 es 40 %, lo que corresponde a la probabilidad de que X sea menor o igual que uno. Debido a que Prob (X > 1) = 1 - Prob (X < 1), decimos que 0,02 forma un 60 % del límite superior de confianza de la no conformidad. El límite superior de la no conformidad no es superior a 0,02, o el 2 % en un 60 % de confianza. Esta probabilidad del 60 % corresponde a la probabilidad de que X sea mayor que uno, o que X sea menor o igual que dos, si p fuera 0,02. Usando nuestra suposición de que p = 0,02, hemos calculado Prob (X < 1) < 0,40, o Prob (X > 1) > 0,60. Nuestro objetivo era encontrar el valor más pequeño de p que nos diera Prob (X < 1) < 0,05, o Prob (X > 1) > 0,95. Claramente, nuestra primera suposición de p = 0,02 no era lo suficientemente grande. Solo hemos movido el 60 % de probabilidad a los valores de X mayores que uno. Nuestro objetivo declarado era calcular un límite superior de confianza del 95 % para p.

Si utilizamos un método de resolución en Excel, podemos estimar que el límite superior de confianza del 95 % para la proporción de no conformidad es de 0,0465598. Lo hacemos resolviendo el binomdist(1, 100, p, 1) = 0,05 para p. Esto da el valor p = 0,0465598 = 4,65598 %. Es decir, binomdist(1, 100, 0,0465598, 1) = 0,05. El valor más pequeño de p que alcanza nuestro objetivo de Prob (X > 1) > 0,95, o Prob (X > 2) > 0,95 es p = 0.0465598.

Ahora, el gráfico de la función de densidad de probabilidad (pdf) se ve así (para los primeros 13 términos).

El gráfico de la función de distribución acumulada (cdf) se ve así (para los primeros 13 términos).

La función de distribución acumulada (cdf) de x = 1 es 40 %, lo que corresponde a la probabilidad de que X sea menor o igual que uno. Debido a que Prob (X > 1) = 1 - Prob (X < 1), decimos que 0,02 forma un 60 % del límite superior de confianza de la no conformidad. El límite superior de la no conformidad no es superior a 0,02, o el 2 % en un 60 % de confianza. Esta probabilidad del 60 % corresponde a la probabilidad de que X sea mayor que uno, o que X sea menor o igual que dos, si p fuera 0,02. Usando nuestra suposición de que p = 0,02, hemos calculado Prob (X < 1) < 0,40, o Prob (X > 1) > 0,60. Nuestro objetivo era encontrar el valor más pequeño de p que nos diera Prob (X < 1) < 0,05, o Prob (X > 1) > 0,95. Claramente, nuestra primera suposición de p = 0,02 no era lo suficientemente grande. Solo hemos movido el 60 % de probabilidad a los valores de X mayores que uno. Nuestro objetivo declarado era calcular un límite superior de confianza del 95 % para p.

Si utilizamos un método de resolución en Excel, podemos estimar que el límite superior de confianza del 95 % para la proporción de no conformidad es de 0,0465598. Lo hacemos resolviendo el binomdist(1, 100, p, 1) = 0,05 para p. Esto da el valor p = 0,0465598 = 4,65598 %. Es decir, binomdist(1, 100, 0,0465598, 1) = 0,05. El valor más pequeño de p que alcanza nuestro objetivo de Prob (X > 1) > 0,95, o Prob (X > 2) > 0,95 es p = 0.0465598.

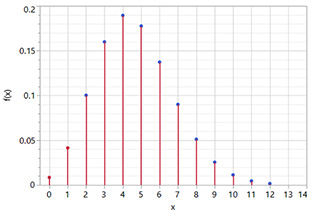Ahora, el gráfico de la función de densidad de probabilidad (pdf) se ve así (para los primeros 13 términos).

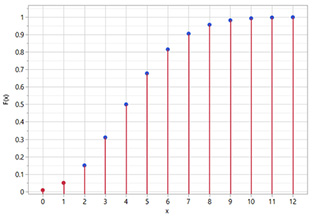
El gráfico de la función de distribución acumulada (cdf) se ve así (para los primeros 13 términos).

Obsérvese que el 95 % de la probabilidad se produce para valores X mayores o iguales que 2, cuando el valor de p es 0,0465598. Prob (X = 2 o X = 3 o … o X = 100) = Prob (X >= 2) = 0,95. Del mismo modo, el cinco por ciento de la probabilidad se produce para valores X menores o iguales que 1. Prob (X = 0 o X = 1) = Prob ( X < = 1 ) = 0,05. Concluimos que un límite superior de confianza del 95 % para la proporción de no conformidades es de 0,0465598, o 4,65598 %.

Para las 900 unidades restantes, estimamos que el 1 % será no conforme, lo cual es 9 unidades; pero podemos decir más que eso. En particular, tenemos un límite superior de confianza del 95 % de que no más del 4,656 % de ellas serán no conformes, lo cual es alrededor de 42 unidades.

En resumen, este artículo ilustra el método para calcular un límite superior de confianza del 95 % para la proporción de no conformidad de las unidades restantes (N - n) que no fueron inspeccionadas, cuando hemos encontrado un total de x unidades no conformes en la muestra aleatorizada de n unidades. Utilizamos un enfoque heurístico, casi didáctico, para explicar cómo se asignaría el 5 % de probabilidad y el 95 % de probabilidad. Hemos estimado el valor del parámetro, p, de una distribución binomial utilizando funciones de Excel y un enfoque de resolución. Este método constituye una valiosa herramienta para el estadístico o el ingeniero de confiabilidad, y es una herramienta muy útil.

Joel Dobson es un científico de datos y estadístico sénior de Texas Instruments, y es miembro del comité de calidad y estadística (E11), donde participa como miembro general del subcomité ejecutivo.

Dean V. Neubauer, coordinador de la columna Data Points, es ingeniero y jefe de estadística en Corning Inc. Es miembro general del subcomité ejecutivo del comité de calidad y estadística (E11), miembro de ASTM International y expresidente del comité E11.