P: Sospecho que mis datos contienen más de un valor atípico. ¿Existe una técnica preferida a usar para aislarlos?

R: Dos técnicas se han analizado en Data Points para probar si una sola observación “con un valor que no parece corresponderse con el resto de los valores en un conjunto de datos” puede ser declarado como un valor atípico. En la columna “Manejo de Valores Atípicos” (Nov. /Dic. 2008) se mencionó el problema asociado con un valor atípico que enmascara a otro valor atípico en una sola prueba de valor atípico y se hizo referencia a la generalización extrema de la desviación de Student (GESD, por sus siglas en inglés) como una técnica sólida e integral para identificar de manera eficaz valores atípicos múltiples. Esta columna proporciona un solo ejemplo del enmascaramiento del valor atípico y cómo aplicar la GESD para identificar valores atípicos múltiples.

Ilustración de Enmascaramiento

Reproduciendo los datos del artículo anterior: [5.3, 3.1, 4.9, 3.9, 7.8, 4.7, 4.3], el valor 7.8 fue visualmente identificado como discordante con el resto de los datos y su valor atípico fue confirmado utilizando la técnica Grubbs comparando su estadística T con un valor crítico, de la siguiente manera:

= promedio = 4.86; s = desviación estándar = 1.48; T7.8 = | 7.8 - 4.86 | / 1.48 = 1.99

Para n = 7 y un riesgo de declaración de falso del 5 por ciento, el valor crítico es 1.938. Ya que T = 1.99 supera este valor crítico, se confirma que 7.8 es un valor atípico.

Supongamos que ahora tenemos el siguiente conjunto de datos: [5.3, 3.1, 4.9, 3.9, 7.8, 4.7, 4.3, 8.0, 4.5, 5.1, 3.5] (consulte el trazado de puntos en la Figura 1). Queremos probar si el valor 8.0 es un valor atípico.

Figura 1 — Trazado de Puntos de datos

Siguiendo el ejemplo del artículo anterior con la técnica de Grubbs, tenemos:

= promedio = 5.01; s = desviación estándar = 1.58; T_8.0 = | 8.0 - 5.01 | / 1.58 = 1.89.

Para n = 11 y un riesgo del 5 por ciento, el valor crítico es 2.234. Ya que T_8.0 = 1.89 es inferior a este valor crítico, no podemos declarar el valor 8.0 como un valor atípico. Por lo tanto, ¿qué ocurrió?

El problema ilustrado anteriormente es un fenómeno que se conoce como enmascaramiento. En este conjunto de datos, los dos valores discordantes visualmente obvios inflaron la desviación estándar, de este modo haciendo que la estadística T sea pequeña en relación al valor crítico.

Uso de GESD para Identificar Valores Atípicos Múltiples

Las técnicas de detección de valores atípicos como Dixon y Grubbs requieren de un examen a priori del conjunto de datos para determinar la cantidad de potenciales valores atípicos y dónde residen (grandes o pequeños) entre los conjuntos de datos. Si existen múltiples valores atípicos, dependiendo del tamaño de estos valores atípicos, las estadísticas de pruebas podrían ser erróneamente pequeñas y dar lugar a una prueba para rechazo insignificante.

Tabla 1 — Cálculos de GESD.

Rosner (1983)¹ propuso una técnica a la que nombró "Procedimiento para Muchos Valores Atípicos con Generalización Extrema de la Desviación de Student (GESD)" para la identificación eficaz de múltiples valores atípicos que no requieren un examen a priori del conjunto de datos para decidir cómo y dónde realizar pruebas para valores atípicos. La comparación detallada de este procedimiento con las otras cuatro técnicas populares fue examinada de forma crítica. La GESD es recomendada en una publicación² de 1993 por la Sociedad Estadounidense de Control de Calidad. Y en 2014, la norma ASTM D7915, Práctica para la Aplicación de la Técnica de Generalización Extrema de la Desviación de Student (GESD) para Identificar Simultáneamente Múltiples Valores Atípicos en un Conjunto de Datos, fue completada por el Subcomité sobre Garantía de la Calidad y Estadísticas D02.94, parte del Comité D02 sobre Productos Derivados del Petróleo, Combustibles Líquidos y Lubricantes. A continuación se realiza una simple descripción de este procedimiento.

Procedimiento de GESD:

1) Decidir a priori el número máximo de valores atípicos a someter a prueba. Llamemos a este número r. (Una recomendación general es establecer r = 20 por ciento de n.)

2) Establecer el índice de ciclo actual i = 1.

3) Calcular la cantidad T = |observación – promedio| ÷ s para cada elemento del conjunto de datos en el círculo actual.

4) Identificar la observación con la cantidad T mayor. Designar esto comoT_1max , max (es decir, T máximo para el primer ciclo).

5) Eliminar la observación identificada en 4) del conjunto de datos.

6) Aumentar el índice i de ciclo actual por 1: es decir, i.e. i = i + 1

7) Repita los pasos 3 a 6 usando los datos restantes hasta e incluyendo i = r.

8) Al finalizar el paso 7, comenzando con T_1max el máximo valor T en ciclo r y trabajando hacia atrás (T_r-1max , T_r-2max .... y así sucesivamente), compare este valor máximo con el valor crítico para el ciclo específico (λi) que se obtuvo de la publicación de ASQC.

9) Identificar el ciclo máximo para el cual T_1max supera su valor límite. La observación asociada conT_1max para ese ciclo y todas las observaciones asociadas conT_1max para todos los ciclos previos hasta e incluido el ciclo 1 se consideran valores atípicos.

Para ilustrar el procedimiento GESD, utilizando el ejemplo anterior, tenemos n = 11 puntos de datos. Por lo tanto, normalmente estableceríamos r = 2 (20 por ciento de n). Sin embargo, con el fin de ilustrar la metodología y mostrar que esta técnica es sólida para la sobre-especificación de r (es decir: más de lo necesario), estableceremos r = 3 para este ejercicio.

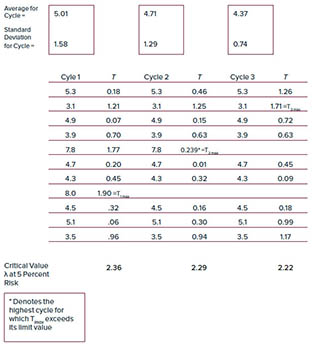
Los cálculos de GESD se mencionan en la siguiente Tabla 1. Ya queT_2max en ciclo 2 es el ciclo máximo que supera su correspondiente valor crítico (λ2), la observación 7.8 para Ciclo 2 y la observación 8.0 para el Ciclo 1 se identifican como valores atípicos.

Referencias

1. Rosner, Bernard, “Percentage Points for a Generalized ESD Many-Outlier Procedure” (Puntos Porcentuales para un Procedimiento de Muchos Valores Atípicos de ESD Generalizados) Technometrics, Vol. 25, N.º 2, mayo de 1983, páginas 165-172.
2. Iglewicz, Boris, and Hoaglin, D.C.,  The ASQC Basic References in Quality Control: Statistical Techiques (Referencias Básicas del ASQC en Control de Calidad: Técnicas Estadísticas), Volumen 16: How to Detect and Handle Outliers (Cómo Detectar y Manejar Valores Atípicos), Quality Press de la American Society for Quality, Milwaukee.

Alex T.C. Lau, TCL-Consulting, Whitby, Ontario, Canadá, es presidente del Subcomité de Coordinación sobre Garantía de la Calidad y Estadísticas (D02.94) y D02.01.0B sobre Precisión, que forman parte del Comité D02 de ASTM sobre Productos Derivados del Petróleo, Combustibles Líquidos y Lubricantes. Miembro de ASTM International, Lau también integra los Comités E11 sobre Calidad y Estadísticas, E36 sobre Acreditación y Certificación y F08 sobre Equipos e Instalaciones Deportivas.