Standardization News:

¿Por qué obtengo tantas señales fuera de control?

Existen varias posibilidades que pueden proporcionar una cantidad mayor de señales fuera de control de la que se puede gestionar razonablemente:

• Caso 1. El proceso está fuera de control de manera que afecta sistemáticamente a varias propiedades del producto a la vez (multiplicidad por correlación).
• Caso 2. Una alta frecuencia de fabricación de productos o de datos implica muchas señales fuera de control (multiplicidad de pruebas o generación de datos). Vea la Figura 1.
• Caso 3. Hay varios parámetros del gráfico de control que colectivamente han aumentado el riesgo de que uno o más parámetros del proceso en control puedan evaluarse como fuera de control (multiplicidad de parámetros).
• Caso 4. La metodología estadística de los gráficos de control asume la normalidad cuando los datos en control no son normales (estadística inadecuada).

Los usuarios de técnicas estadísticas presuponen que los estadísticos ya han realizado todas las tareas por ellos. Después de todo, han proporcionado reglas bien definidas para crear gráficos de control de varios tipos y reglas bien definidas para su interpretación. ¿Qué podría salir mal? Sin embargo, los estadísticos no han hecho sus tareas de gestión de riesgos. En general, le advierten sobre los supuestos de distribución que, cuando se infringen adecuadamente, pueden proporcionar el Caso 4 para una alarma excesiva. Lo que no suelen advertir son los Casos 1, 2 y 3, los escenarios en los que el procedimiento de gráfico de control se aplica frecuentemente (multiplicidad) en cierto contexto de pruebas. Y el monitoreo es, de hecho, la realización repetida de pruebas.

Esto se debe en parte a que los estadísticos, a menudo, se ven a sí mismos solo como gestores de riesgos del algoritmo proporcionado, en lugar de gestores de riesgos de cómo se aplican de manera extendida estos algoritmos en la práctica. Muchos otros procedimientos estadísticos presentan problemas de gestión de riesgos en aplicaciones específicas, incluso a veces cuando los utiliza un estadístico, pero este artículo se centra en los gráficos de control.

El Caso 1 se produce cuando algunos o muchos de los parámetros de los gráficos de control están correlacionados debido a la naturaleza inherente del proceso de fabricación, muestreo o medición. Es probable a que todos se deban a la misma causa raíz o al mismo artefacto de medición. A veces, la correlación es un artefacto del tipo de sistema de medición o del sistema de muestreo de mediciones cuando un sistema de medición determina simultáneamente varias mediciones físicas trazadas.

Los Casos 2 y 3 serán el principal foco de atención de este análisis. En el Caso 2, imaginemos una única medición para monitorear el desempeño del sistema que se mide de forma automática cada 4 minutos. Además, suponga que se está utilizando un gráfico de control individual de Shewhart, con los límites estándar de 3 sigmas, para monitorear el proceso. En un día habrá 15x24 = 360 mediciones, cada una con una probabilidad aproximada de 1/370 de dar una señal fuera de control. Esta frecuencia proporcionará, solo por casualidad, un promedio de casi una señal de alarma fuera de control al día (360/370) cuando el sistema esté en control.

En la Figura 1, se presenta un ejemplo de un día de datos en control a partir de nuestro hipotético sistema simulado y representado en un gráfico. Note que se observan tres señales fuera de control. Hay cerca de 7,5 % de probabilidades de que se observen tres o más señales de alarma fuera de control para el escenario en control descrito. Solo hay un 38 % de probabilidades de que no se observe ninguna señal fuera de control en un día. Si se empleara cualquier versión del conjunto de reglas de Western Electric junto con el gráfico de control de Shewhart, se produciría un considerable aumento de las señales de alarma múltiples diarias por mera casualidad.

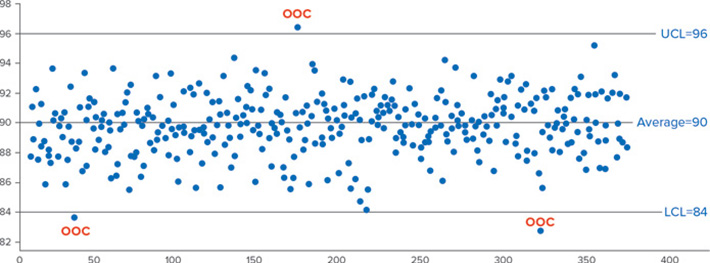
Figura 1: Impacto de la alarma de datos de alta frecuencia en control

En el Caso 3, imagine que mide y hace un gráfico de control de 40 parámetros y produce 9 lotes diarios (9x40 = 360 mediciones diarias). Esto es aproximadamente similar en términos de riesgo al escenario anterior del Caso 2, siempre que los 40 parámetros no estén muy interrelacionados.

Un breve artículo como este no puede describir por completo las mejores formas de solucionar este problema de gestión del riesgo sistémico (Casos 2 y 3). Puede servir para considerar el problema como un tema de asignación de recursos para la mejora o el sostenimiento de los procesos. Si hay una gran cantidad de señales que no parecen estar relacionadas con una causa asignable, elija un multiplicador sigma mayor que 3 para declarar el proceso fuera de control. Elija un multiplicador que proporcione una tasa manejable de señales fuera de control falsas, pero no tan grande como para crear un riesgo inaceptable de falla del proceso. Así se reducirá el índice de señalización fuera de control y se podrán priorizar las grandes desviaciones del proceso para mejorarlo.

Si con estos esfuerzos no se logra ninguna mejora del proceso y este no se degrada, se podría considerar la posibilidad de aplicar un multiplicador sigma aún mayor para el nivel de alarma. No obstante, nunca debe fijarse tan alto que coloque el nivel de alarma cerca de un modo de falla conocido. Tenga en cuenta que se pueden producir fallas tanto en su proceso de producción como en el de su cliente. Por tanto, la evaluación de los modos de falla y del riesgo también debe extenderse a los procesos de su cliente. Si la mejora del proceso se logra a lo largo del tiempo, considere el valor de reducir el multiplicador más cerca de 3 que del multiplicador ampliado descrito previamente.

Los párrafos anteriores describen un planteamiento pragmático para alcanzar lo que se espera obtener del gráfico de control combinado con la aplicación del análisis de causas raíz. Desde el punto de vista intelectual, es controvertido porque se aleja de la práctica habitual. Sin embargo, la práctica común actual fracasa desde la inexperiencia ante la multiplicidad.

La disminución del excesivo impacto de alarma debido a la multiplicidad en el caso de varios parámetros también puede abordarse mediante algoritmos de reducción de la dimensionalidad. Los gráficos resultantes son multiparámetro. La reducción de la dimensionalidad puede ocultar cambios en variables individuales que aún requieren cierto nivel de monitoreo. Se recomienda un enfoque híbrido de límites siempre que se reduzca la dimensionalidad de los datos por medio de cualquier metodología. En un enfoque híbrido, también se mantienen gráficos de variables individuales, pero con límites superiores a 3 sigmas.

Las alarmas excesivas de la aplicación de gráficos de control jamás deben ignorarse, más bien deben abordarse de manera adecuada. Si la multiplicidad está presente con la intensidad suficiente, es necesario abordar la situación para no desperdiciar recursos persiguiendo fantasmas estadísticos. A menudo, se considera, erróneamente, que la gestión de un sistema moderno de calidad, rico en datos, es todavía de naturaleza formulista. La multiplicidad nunca debe ignorarse. ■

Thomas Bzik, StatsOnTheGo, Inc., es miembro y expresidente del Comité de calidad y estadística (E11). Por sus servicios, recibió premios de reconocimiento del E11 y del Comité de calidad del aire (D22).

El Dr. John Carson es estadístico sénior de Neptune and Co. y coordinador de la columna Data Points. Es miembro de los comités de Calidad y estadísticas (E11), Productos derivados del petróleo, combustibles líquidos y lubricantes (D02), Calidad del aire (D22) y otros.