Impacto de la heterogeneidad de la variabilidad de las mediciones en la calibración y los gráficos de control

Por Thomas J. Bzik

P. ¿Afecta la heterogeneidad del sistema de medición el análisis estadístico?
R. Sí, esta heterogeneidad puede influir de manera significativa en todas las técnicas básicas de análisis estadístico. Por lo general, las técnicas estadísticas básicas utilizan las suposiciones de homocedasticidad y normalidad con fines de simplificación. La homocedasticidad es la expectativa de que todas las mediciones de muestras, a priori, se determinan con el mismo grado de incertidumbre aleatoria (que se originan a partir de una distribución con la misma varianza/desviación estándar). La heterocedasticidad es la falta de homocedasticidad.

Calibración

Los instrumentos analíticos modernos rara vez tienen en cuenta la escala de interés de manera directa. En cambio, miden una propiedad física que puede estar relacionada con la escala de interés a través de una calibración. En un análisis de calibración típico, se miden los niveles “conocidos” de un estándar de trabajo en el sistema que se calibrará. A menudo se utiliza el análisis de regresión por mínimos cuadrados con dichos datos para establecer la calibración. Este modelo permite que las mediciones futuras en la escala de medición del instrumento se vuelvan a convertir matemáticamente a la escala más útil de los estándares. La calibración permanece oculta a los consumidores de los datos del instrumento, ya que solo ven las mediciones expresadas en las unidades de interés. Toda deficiencia en un proceso de modelado de calibración ya está integrada a los resultados medidos.

La calibración por mínimos cuadrados es sensible a la presencia de heterogeneidad del sistema de medición. La figura 1 ilustra un modelo de calibración lineal para un patrón ascendente de heterocedasticidad del sistema de medición. El análisis de regresión por mínimos cuadrados estándar supone una homocedasticidad y se ajusta al modelo de calibración en el supuesto de que todos los puntos se miden con la misma confiabilidad. Esto lleva a que los puntos con menor incertidumbre (lado izquierdo) infraponderen de manera relativa en el ajuste del modelo y a que los puntos con mayor incertidumbre se sobreponderen de manera relativa en el ajuste del modelo cuando la heterocedasticidad no se aborda en el análisis de regresión. En los casos en que la variabilidad es menor, es posible que el modelo de calibración por mínimos cuadrados no pase por los datos o lo suficientemente cerca, en términos estadísticos, de los datos en este nivel, relativamente hablando. Se requiere un análisis de mínimos cuadrados ponderados o un enfoque de regresión de variables para obtener una estimación razonable de la calibración en este escenario.

Una situación de medición relativamente de rutina en la que es probable que dicha variación heterogénea en la medición se aplique es en los sistemas de medición del nivel de trazas. En este caso, las mediciones se suelen realizar en los niveles de parte por millón (ppm), parte por mil millones (ppb), y los sistemas de ppb son más propensos a demostrar una versión más sólida de heterocedasticidad que los sistemas de ppm. Un patrón típico desencadena un patrón creciente de variabilidad a medida que aumenta la concentración estimada.

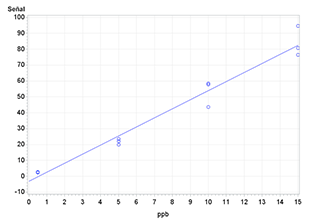
Figura 1. Calibración utilizando un análisis de regresión por mínimos cuadrados en presencia de una heterocedasticidad

La interpretación de los intervalos de confianza del modelo de regresión y todas las interpretaciones de importancia estadística se corrompen una vez que la heterocedasticidad se torna relativamente significativa y los mínimos cuadrados se fuerzan. Tal como ilustra la figura 1, el extremo izquierdo de la calibración puede desplazarse con respecto de los datos. Por ejemplo, se pueden obtener intersecciones negativas inesperadas o, incluso, estimaciones negativas inesperadas de concentración a partir de un escenario de ajuste de calibración defectuoso. Si no se aborda la heterogeneidad de la variación en la calibración, se introduce un sesgo sistemático en la calibración. En términos de la estimación de parámetros modelo para el escenario de la creciente heterocedasticidad ilustrado, la estimación de pendiente no es propensa a sesgarse de manera significativa. Sin embargo, la intersección suele sesgarse de manera significativa¹,². Esto introduce un sesgo en la parte izquierda (niveles más bajos) de la curva de calibración, lo cual corromperá aún más la estimación de los límites de detección. La heterocedasticidad de medición no abordada tiene un impacto relativamente importante en la calibración.

Gráficos de control de personas de Shewhart

El impacto de la variación del sistema de medición en los gráficos de control, que supone, de manera implícita, una homogeneidad de variación en su construcción, es más complejo. Para fines de debate, supongamos que hay dos fuentes de variación: la del proceso de fabricación y la del proceso de medición. Supongamos que el proceso de fabricación proporciona una distribución normal con cierta desviación promedio y estándar σ1. Asimismo, supongamos que el sistema de medición es no sesgado y tiene cierto error constante normalmente distribuido σ2. En este escenario de varianza en el error de homogeneidad de la medición, resulta apropiado aplicar la teoría normal a la combinación combinada de estas dos fuentes de error en los gráficos de control.

Cuando se encuentra una homogeneidad en la variación de medición, el escenario más común es que la variación de medición aumente, en cierta manera, con la magnitud de la propiedad que se está cuantificando. Con una heterocedasticidad de medición, la distribución resultante de los datos para los que se están confeccionando gráficos de control se vuelve no normal a pesar de la misma suposición de normalidad para la variación de fabricación y la suposición de normalidad, pero con una desviación estándar diferencial, para cada valor medido. Con dicha heterocedasticidad de medición, la cola inferior de la distribución observada se torna relativamente más corta en promedio y la cola superior se vuelve relativamente más larga en promedio. Si el intervalo relativo de heterocedasticidad de medición es lo suficientemente pequeño respecto de la variación de fabricación, es posible que esta consecuencia no sea de importancia práctica.

Los problemas de confección de gráficos de control se producen cuando un proceso de fabricación se controla de forma más estrecha de lo que se puede medir de manera confiable (capacidad del sistema de medición deficiente) y se anticipa enérgicamente una homogeneidad de medición. Estos dos factores se encuentran con cierta frecuencia en contextos de medición de contaminación de trazas en los que el principal objetivo de fabricación es la ausencia de múltiples contaminantes posibles en niveles de trazas. Algunos contaminantes en niveles de trazas ni siquiera se anticipan, pero se miden y “controlan” por pura precaución. Otros contextos de medición de datos no descritos también podrían resultar relevantes.

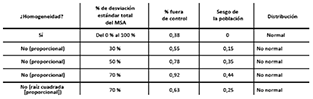
Tabla 1. Índices fuera de control con un límite de control superior de personas de Shewhart cuando n = 30

La tabla 1 ilustra, de manera simultánea, el impacto de varios escenarios de variación de medición y escenarios de capacidad de medición para una muestra de 30 unidades. Con la homogeneidad, el porcentaje fuera de control (OOC) esperado y el sesgo de la población no se ven afectados por ningún resultado en todo el intervalo de capacidad de medición del 0 % al 100 % (los elementos afectados no se estudian en este documento). La heterogeneidad proporcional y la heterogeneidad proporcional de la raíz cuadrada, respectivamente, indican que, al momento de medir un valor del doble de tamaño, este tendrá el doble de desviación estándar de la medición y √2 veces la desviación estándar de la medición. Asimismo, en la práctica general del escenario de contaminación a niveles de trazas, con frecuencia solo se estudian los límites de control superiores.

El riesgo de teoría normal normalizado en función de los cuatro porcentajes de heterogeneidad fuera de control expresados en tablas sería el riesgo equivalente a tener gráficos de control individuales confeccionados que solo utilizaran 10 de las 14 observaciones normalmente distribuidas. La heterocedasticidad de medición, con su asimetría inducida, incluso con suposiciones de normalidad impuestas en todas las distribuciones de muestras (de proceso y de medición), afecta de manera adversa la calibración, la estimación del límite de detección y, a veces, la estimación del límite de control.

Referencias
1. Ketkar, S.N., y Bzik, T.J., “Calibration of Analytical Instruments. Impact of Nonconstant Variance in Calibration Data,” Analytical Chemistry, vol. 72, n.º 18 (2000), págs. 4672-4765.
2. Bzik, T. J., “Calibration,” Encyclopedia of Statistics in Quality and Reliability, John Wiley & Sons, Hoboken, N.J., 2008.

Thomas J. Bzik es el actual presidente del Comité de Calidad y Estadística (E11) y trabaja como consultor estadístico.

Dean V. Neubauer, es ingeniero adjunto y jefe de Estadística de Corning Inc., y coordinador de la columna Data Points. Es miembro general del subcomité ejecutivo del comité sobre calidad y estadística (E11), miembro de ASTM International y expresidente del comité E11.