Importancia de datos

La comprensión de la significación estadística y práctica

Por Thomas J. Bzik

P. ¿Cuál es la diferencia entre la estadística y la significación práctica?

R. Muchas de las normas de ASTM basadas en datos utilizan datos pertinentes, junto con una prueba o varias pruebas de significación estadística como su principal medida de interpretación. En este sentido son análogas a la mayoría de los ejemplos que se encuentran en los libros de texto de estadística, los cuales se centran principalmente en la significación estadística. Esta puede ser una perspectiva muy limitada. En este artículo se expone otro tipo de significación, la significación práctica, y su interrelación con la significación estadística. La comprensión de los problemas estadísticos simultáneamente en el contexto de los dos tipos de significaciones es de gran utilidad. 

Dos aplicaciones habituales de significación estadística en las normas ASTM involucran la prueba de la significación estadística para buscar una diferencia estadísticamente significativa entre las medias y las varianzas de dos muestras. Las pruebas de significación estadística conducen a una decisión binaria, se identifica una diferencia estadísticamente significativa entre las medias y las varianzas o no. La significación estadística indica que se ha identificado evidencia estadísticamente fuerte de una diferencia real medible entre los grupos de prueba. La falla al obtener la significación estadística es una conclusión más débil, que indica que no se ha identificado una diferencia estadísticamente significativa. No hay una conclusión fuerte de que sean iguales, sólo que la diferencia observada no es lo suficientemente grande como para ser considerada estadísticamente diferente. En la práctica, a menudo se considera que de no encontrar significación estadística, no hay diferencia o necesidad de nuevas acciones. 

A modo de ejemplo, supongamos que la prueba de ASTM tiene por objeto establecer la equivalencia de dos conjuntos de datos.  La metodología estadística da lugar a dos posibles conclusiones. La primera es una hipótesis nula de que no hay diferencia entre los dos conjuntos de datos y una hipótesis alternativa de que los dos conjuntos son diferentes.  Por ejemplo, si la prueba estadística elegida es comparar las varianzas de cada uno de los dos conjuntos de datos, se utiliza una prueba F. Nuestro enfoque es la naturaleza binaria de los resultados de la prueba de hipótesis. En la prueba de hipótesis, si las varianzas difieren suficientemente en términos de una distancia estadística, la prueba indicaría evidencia estadísticamente significativa de una diferencia, y la hipótesis nula sería rechazada. Los conjuntos de datos se considerarían no equivalentes. Alternativamente, si la diferencia no puede ser considerada estadísticamente significativa, se acepta la hipótesis nula de no diferencia en la práctica común. Por tanto, si un procedimiento de ASTM no incorpora la significación práctica, los dos conjuntos de datos serían juzgados como equivalentes. 

La significación práctica es otro concepto de significación binaria que es independiente de la significación estadística. La significación práctica consiste en mirar el tamaño de la diferencia observada en el contexto del problema. Si esta diferencia de tamaño es consecuente, entonces se dice que la diferencia tiene una significación práctica; de otro modo no. Estos dos tipos de juicios de significación binarios conducen a una tabla de 2x2 de posibles resultados (Tablas 1 y 2).  En la Tabla 1 los resultados de significación están de acuerdo o en desacuerdo. La Tabla 2 expresa a la Tabla 1 en términos de si se requiere tomar nuevas medidas. 

Consideremos cuando la significación estadística y práctica están de acuerdo. Si hay tanto significación estadística como práctica, entonces las distribuciones representadas por las muestras deben ser tratadas como diferentes en el contexto de la aplicación. Cuando no hay ni significación estadística ni práctica, entonces se deben tratar las distribuciones en cuestión como esencialmente equivalentes en el contexto de aplicación. 

Cuando las medidas de significación discrepan, las cosas se ponen más interesantes. 

Consideremos donde hay significación estadística, pero no significación práctica. Aquí existe una fuerte evidencia basada en los datos de una diferencia medible, pero la diferencia se considera que tiene un impacto demasiado pequeño como para actuar en consecuencia. Por ejemplo, al probar la equivalencia de la desviación estándar de un nuevo instrumento analítico con el proceso de registro de la desviación estándar se encontró una diferencia estadísticamente significativa. El nuevo instrumento tiene una desviación estándar observada de 2.6 ppb, y el proceso de registro tiene una desviación estándar observada de 2.4 ppb. Supongamos que el fabricante del instrumento ha declarado que la desviación estándar del instrumento puede variar de un instrumento a otro hasta en 0.5 ppb. Aquí la diferencia observada no es prácticamente significativa en relación con el proceso de fabricación del instrumento. Tratar de solucionar el problema del instrumento sería poco aconsejable. No es que no se haya identificado una diferencia medible, es que la adopción de nuevas medidas a causa de este resultado es cuestionable a menos que el fabricante del instrumento fuera a mejorar el instrumento en cuestión. Aquí la significación práctica sirve como un juicio de valor que establece que abordar la diferencia estadísticamente significativa es de un valor o practicidad relativamente limitados. Este escenario se vuelve más probable con muestras de mayor tamaño. El uso de más datos permite identificar diferencias relativamente más pequeñas como estadísticamente significativas.

Tabla 1 — Significación Estadística vs. Significación Práctica.

Consideremos ahora el caso en el que no se encontró significación estadística, pero el resultado es de significación práctica (el caso de color rojo en las Tablas 1 y 2). Sigamos con el ejemplo del instrumento, pero ahora el nuevo instrumento tiene una desviación estándar observada de 5.3 ppb, pero se encontró que no hubo diferencias estadísticas significativas de 2.4 ppb. Supongamos que el ingeniero de proceso sabe que si la desviación estándar del instrumento es realmente 5.3 ppb, esto implica que se espera que el 8 por ciento del producto futuro esté fuera de la especificación exclusivamente debido a este aumento de la incertidumbre analítica. Si la desviación estándar es realmente de 5.3 ppb, entonces esto se traduce en $30 millones de dólares menos de producto para vender al año (por ejemplo, la diferencia es de significación práctica). En este caso, la diferencia observada, si es real, es consecuente, pero la falta de significación estadística implica que la diferencia observada puede haber sido resultado únicamente de ruido de datos. Es más probable que ocurra esta situación con muestras de tamaños más pequeños que con muestras de mayor tamaño. La acción apropiada es recolectar más datos. Con suficientes datos adicionales, el problema se habrá resuelto. Con datos adicionales, ya sea (1) la diferencia observada disminuirá por debajo de la significación práctica o (2) los datos adicionales harán que el resultado sea estadísticamente significativo. Una vez que las medidas de significación de uno o ambos cambien, el problema se resuelve.

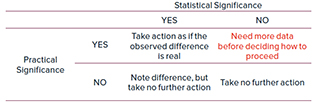
Tabla 2:  Versión de Acción de la Tabla 1.

Una norma de ASTM que incorpora aspectos de significación práctica es la E2935, Práctica Estándar para la Realización de Pruebas de Equivalencia en Aplicaciones de Laboratorio. Muchas de las prácticas estándar para las pruebas de equivalencia en las normas de ASTM no tienen el nivel de sofisticación de pruebas que tiene la E2935. El artículo de DataPoint, Pruebas de Equivalencia: Por qué Funciona el Procedimiento TOST, contiene material de lectura adicional útil tanto sobre significación práctica como estadística.¹

Los métodos estadísticos son herramientas muy valiosas si el enfoque no se reduce artificialmente al centrarse únicamente en la significación estadística. Use las dos medidas de significación con juicio.

Thomas J. Bzik, consultor estadístico, Macungie, Pennsylvania, cumple la función de vicepresidente del E11 sobre Calidad y Estadística, y de presidente del Subcomité E11.10 de Muestreo/Estadísticas.

Referencias
1. Murphy, T.D., Testing for Equivalence: Why the TOST Procedure Works, ASTM Standardization News, Sept./Oct. 2014, Vol. 42, No. 5, pp. 16-17.