Modelos de probabilidad para epidemias y materiales

Por Peter Fortini

P: ¿Cómo nos ayuda el conocimiento de los materiales a entender una epidemia?

R: En el transcurso de la pandemia actual por la COVID-19, los periódicos han publicado gráficos que muestran cómo las cifras de casos nuevos en diversos países, regiones o estados aumentan, se mantienen nivelados y disminuyen y, luego, tal vez, vuelven a aumentar. En el afán de entender lo que está sucediendo, nos valemos de la capacitación y los conocimientos que tenemos. Existen analogías cercanas cuando analizamos la estructura de algunos de los materiales de interés para ASTM International y en los estándares de ASTM.

En ASTM, nos encontramos con estadísticas, principalmente, en el contexto de la definición de la repetibilidad y reproducibilidad de los métodos de prueba, los diagramas de control para procesos, el muestreo de aceptación, la calibración y, tal vez, el diseño de experimentos. No obstante, el estudio de las estadísticas también incluye una gran dosis de procesos estocásticos y teoría de la probabilidad.

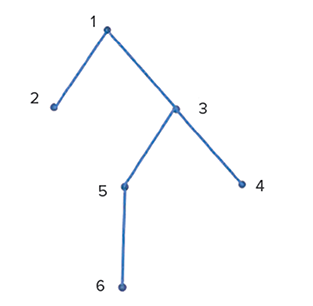
Figura 1: Obtención de un proceso de ramificación

Un ejemplo clásico de proceso estocástico es el proceso de ramificación de Galton-Watson. Este proceso comienza con un individuo, que tiene ninguno, uno o más (un número aleatorio) “descendientes” para la siguiente generación. El número de descendientes está dado por una distribución de probabilidad, p0, p1, p2 etc. Cada uno de ellos, a su vez, produce un número aleatorio de individuos para una tercera generación y así sucesivamente. En el proceso de ramificación de Galton-Watson, el número sigue la misma distribución de probabilidad.

Este modelo de probabilidad, creado por Francis Galton, se aplicaba originalmente a la supervivencia o reproducción de los apellidos de familia, donde la descendencia relevante de un individuo es la cantidad de hijos que portarán el apellido de la familia. En genética, un caso adicional es la supervivencia y reproducción de un gen mutante, donde el número promedio de descendientes es una medida directa de la “aptitud” del gen mutante. Otros ejemplos que se proporcionan en textos clásicos sobre probabilidad son las reacciones nucleares en cadena y la longitud de las colas de espera (donde los “descendientes” de un individuo al que están atendiendo son las personas que se unen a la cola mientras lo atienden).¹ Una epidemia es otro ejemplo más del proceso, en el que los descendientes de un individuo infectado son las personas adicionales a las que este individuo infecta.

Las siguientes son las características básicas de este proceso:

• Existe una probabilidad p0 de que el individuo inicial no tenga descendientes para la siguiente generación, por lo cual el proceso se extingue de inmediato.
• Existe una probabilidad de que la cadena se extinga incluso aunque el individuo inicial tenga descendientes. Esto sucederá siempre que la media de μ (en epidemiología, la tasa de reproducción R0) de la distribución de los descendientes de un individuo sea menor que uno.
• Si la media de la distribución de los descendientes es mayor que uno, existe una posibilidad de que el número crezca de manera exponencial. Todavía hay posibilidades de que se extinga. La probabilidad de una eventual extinción se determina en la teoría del proceso de Galton-Watson como la raíz menor que 1 de la siguiente ecuación que incluye la función de generación de probabilidad de la distribución de los descendientes.

Con una media mayor que uno, una vez que el número de individuos de una generación es lo suficientemente alto, el crecimiento, para fines prácticos, es exponencial con los siguientes datos:

cantidad de individuos de la n.ª generación = k exp. (μ n)

donde k depende de la variación que se produzca en las etapas iniciales.

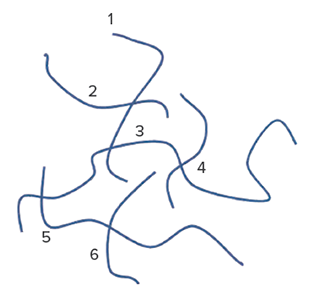
Figura 2: Una red de polímero

Por supuesto, un crecimiento exponencial ilimitado no puede mantenerse por mucho tiempo en ningún proceso real. Habrá un límite de recursos. En el caso de una epidemia, es la población de personas que podrían estar expuestas. Para una reacción en cadena, es la cantidad de material nuclear inicial, así como su dispersión en la explosión posterior.

En el contexto de los materiales, ¿dónde observamos procesos similares? Otros ejemplos importantes forman parte de la ciencia de polímeros y se describen en el texto clásico de Flory.² Muchos materiales, como las resinas, los revestimientos, los plásticos y el caucho, están compuestos por moléculas que nacen como largas cadenas lineales que se unen a través de enlaces cruzados.

El proceso de ramificación se aplica a los materiales de la siguiente manera.

Suponga que empezamos con una unidad (monómero) seleccionada al azar en un material de este tipo. Consideramos que la cadena lineal en la que se encuentra es el individuo inicial. Sus “descendientes” son las cadenas adicionales que se conectan a ella mediante enlaces cruzados o ramificaciones. Las figuras 1 y 2 muestran la comparación. Para que resulte más simple, muestra un caso en el que el proceso se extingue. El conjunto entero de cadenas que se obtiene siguiendo los enlaces cruzados (combinando generaciones) es la porción del material conectada a la unidad seleccionada en un principio. En una resina sin curar, oligomérica, la cantidad promedio de cadenas adicionales conectadas a una unidad inicial es menor que uno. Cuando un material se cura, la cantidad promedio de enlaces cruzados o ramificaciones de una cadena aumenta a mayor que uno. Entonces, el crecimiento exponencial significa que la unidad inicial forma parte de una red efectivamente infinita. El punto de gelificación es el punto de curado en el que aparece la red infinita por primera vez. No mucho después de comenzar el proceso de curado de los materiales poliméricos reticulados, la mayor parte del material está compuesta por una sola molécula grande. La probabilidad de la extinción final desde la unidad aleatoria inicial, para el material, nos brinda la fracción que no está conectada a esta red (parte de la cual podría ser, por ejemplo, extraíble).

Si aplicamos esta analogía a la propagación de una epidemia o pandemia, ilustra que, en un caso no controlado, prácticamente la totalidad de la población susceptible, con el tiempo, se infectará a partir de un primer caso y solo una porción relativamente pequeña no estará vinculada con la red de contagio.

Muchos de los gráficos que siguen la evolución de la pandemia actual por la COVID-19 muestran una disminución posterior a los incrementos iniciales en la cantidad de casos. De acuerdo con la analogía de las redes de los materiales poliméricos, solo deberíamos esperar que esto ocurra cuando la amplia mayoría de la población se haya infectado. Sin embargo, las cifras totales continúan siendo solo una fracción de eso.

¿Qué hay detrás de las disminuciones que observamos? Es posible que las disminuciones se deban, en parte, a la distancia geográfica entre las regiones que informan sus cifras y, en parte, a la fragmentación social general, donde los miembros de nuestra sociedad que pertenecen a subgrupos tienen relativamente poco contacto entre sí y, de esta manera, no se ven afectados (todavía). Sin embargo, no hay duda de que las disminuciones son, principalmente, producto de las medidas que se han adoptado: cancelación de reuniones grandes, uso mascarillas cuando tenemos contacto con el público general, trabajo desde casa y otras medidas de distanciamiento social, para reducir la media de la distribución de los descendientes de manera directa.

Las similitudes entre fenómenos que aparentan ser muy diferentes se vuelven evidentes cuando se describen en términos matemáticos. Lo que uno ya sabe de uno o más de estos temas nos ofrece un punto de partida para comprender otros nuevos.

Referencias
1. Feller, William, An Introduction to Probability Theory and Its Applications, Vol. 1, Wiley, New York, 3rd edition, 1968 (first edition 1950).
2. Flory, Paul J. Principles of Polymer Chemistry, Cornell University Press, Ithaca, New York, 1953.

Peter E. Fortini es el vicepresidente del comité de calidad y estadística (E11), en el que también se ha desempeñado como presidente. Es un miembro asociado de ASTM International y ha recibido el Premio al Mérito.

Dean V. Neubauer, es ingeniero adjunto y jefe de estadística de Corning Inc., y el coordinador de la columna Data Points. Es miembro general del subcomité ejecutivo del comité de calidad y estadística (E11), miembro de ASTM International y expresidente del comité E11.