Potencia y tamaño de la muestra, parte 1
P.: ¿Cuántas muestras debo probar?
R.: La selección del tamaño correcto de la muestra requiere que un estadístico tenga en cuenta varias variables. Si realiza muy pocas pruebas, corre el riesgo de perder potencia estadística y la capacidad de detectar una diferencia significativa. Si realiza demasiadas pruebas, corre el riesgo de desperdiciar recursos y afectar el cronograma del proyecto. La clave es detectar una diferencia significativa, dadas las probabilidades de error razonables. La muestra debe representar suficientemente a la población para las pruebas de hipótesis. Las pruebas de hipótesis determinan si algo es estadísticamente igual (hipótesis nula) o diferente (hipótesis alternativa). Los tamaños de muestra deben poder detectar una diferencia mínima práctica para una potencia dada. Este artículo analiza los datos de entrada para estos cálculos estadísticos, seguido de un ejemplo para consolidar los conceptos.
Los factores para determinar el tamaño de la muestra son intuitivos. Los tamaños de muestra más grandes detectarán una diferencia más pequeña. Hay rendimientos decrecientes a medida que aumenta el tamaño de la muestra. El tipo de datos también influye en el tamaño de la muestra. Las variables continuas requieren un tamaño de muestra mucho más pequeño que las muestras de pasa/no pasa (atributo). También son necesarias estimaciones para la población, como la desviación estándar o la proporción defectuosa. Si se puede reducir la variabilidad, también se puede reducir el tamaño de la muestra.
Esta comprensión intuitiva también se puede expresar a través de una serie de ecuaciones. Comenzando con la ecuación 26 de la práctica para calcular y usar estadísticas básicas (E2586):
donde:

Esta ecuación para el tamaño de la muestra (n) armoniza con la intuición mencionada anteriormente.
El tamaño de la muestra (n) y el margen de error (ME) son inversamente proporcionales, por lo que un margen de error más estrecho generará un tamaño de muestra más alto. De forma inversa, el tamaño de la muestra (n) y la desviación estándar de la población (σ) son directamente proporcionales, por lo que una desviación más alta generará un mayor tamaño de muestra.


Z supone una σ (desviación estándar de la población) conocida. Para tamaños de muestra más pequeños, es importante reemplazar Z por una t. Este cálculo aumenta en complejidad, ya que el valor t depende del tamaño de la muestra, por lo que este método generalmente emplea un software estadístico como Minitab.
Una curva de potencia puede expresar visualmente este cálculo. La Figura 1 muestra una curva de potencia para una prueba t de una muestra usando datos de entrada comunes (bilateral, α = 0.05, potencia = 0.90, desviación estándar = 1.0, ME = 0.5, 1.0 y 2.0).
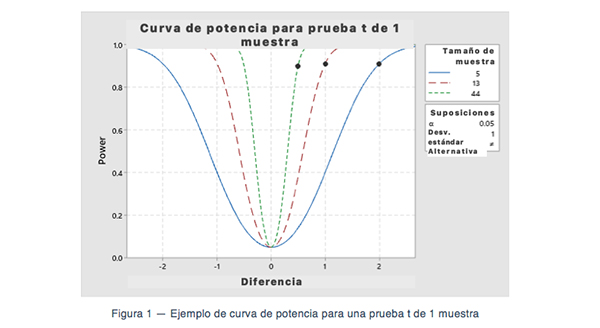
Los puntos de la Figura 1 muestran las diferentes intersecciones que cumplen con la condición de potencia de 0.9 requerida. La potencia cambia a medida que nos alejamos de la diferencia 0 (o de la hipótesis nula). La figura 1 muestra específicamente que el tamaño de la muestra aumenta de 5 a 13 y hasta 44 cuando la diferencia mínima detectable disminuye de 2 a 1 y a 0.5. Esto ilustra la compensación entre el tamaño de la muestra y la detección de una diferencia más pequeña a una potencia dada.
Un ejemplo del uso de la potencia y el tamaño de la muestra en la práctica:
Problema: una empresa anuncia que sus cajas de cereal contienen 13 onzas de producto. Ingeniería cumplimentó recientemente una reparación en el equipo de llenado. Usted debe verificar que esto no afectó el peso de llenado (medio) y que permanece en el objetivo de 13 onzas. Ingeniería establece que un peso medio dentro de ± 0.1 onzas no tiene ninguna diferencia práctica. Ingeniería no conoce la desviación estándar de los pesos y establece que el rango de los pesos es 12.5 – 13.5 oz. Se determina usar una diferencia de 0.1 y que α = 0.10 y potencia = 0.80 es razonable dado el riesgo.
Solución de muestreo: usted necesitará saber si el peso medio está en el peso objetivo de 13 onzas utilizando una prueba t de 1 muestra. La desviación estándar se estima a partir del rango de 1 onza. Una suposición razonable es utilizar 1/6 del rango para obtener una desviación estándar estimada de 0.167 onzas. (Referencia E122-17, Figura 1, para esta regla general a estimar). El software calcula un mínimo de 19 cajas de cereal que se pesarán para la prueba de hipótesis. Ingeniería afirma que pesarán 20. Ingeniería proporciona los datos en el mismo orden en que salen del equipo de llenado en caso de un escenario poco probable, como el cambio o la desviación de los datos.

Carol Parendo es miembro de Collins Aerospace y miembro del subcomité ejecutivo del Comité sobre Calidad y estadística (E11).
El Dr. John Carson, estadístico sénior de Neptune and Co., es el coordinador de la columna Data Points. Es miembro del Comité sobre Calidad y estadística (E11), así como de los Comités sobre Productos derivados del petróleo, combustibles líquidos y lubricantes (D02), Calidad del aire (D22) y Evaluación ambiental, gestión de riesgos y medidas correctivas (E50).
 Página Principal
Página Principal Archivo
Archivo La Mancheta
La Mancheta Enviar correo electrónico al editor
Enviar correo electrónico al editor Calendario Editorial (Inglés)
Calendario Editorial (Inglés)