Precisión en los Métodos
de Prueba de la ASTM

Qué Significa la Precisión

Por John Carson

P: ¿Qué es la precisión y cómo se interpreta en el contexto de los métodos de prueba de la ASTM?

R: A partir de la norma ASTM E177, Práctica para el Uso de los Términos de Precisión y Sesgo en los Métodos de Prueba de la ASTM, tenemos esta definición de precisión:
Precisión: el grado de concordancia entre los resultados de pruebas independientes obtenidos bajo condiciones especificadas.

Lo que en realidad se mide es la imprecisión, generalmente por medio de la desviación estándar, que tiene una relación inversa con la precisión. Para un proceso en el control estadístico con una única causa común y ninguna variación de causa especial, y siguiendo la distribución normal, la desviación estándar (denotada por σ) es una excelente medida de dispersión.

La frase “obtenidos bajo condiciones especificadas” es muy importante. Las normas definen las condiciones comúnmente especificadas como:
Condiciones de repetibilidad: condiciones en las cuales el mismo operador obtiene resultados de pruebas independientes con el mismo método aplicado a objetos de prueba idénticos en el mismo laboratorio utilizando el mismo equipo dentro de intervalos breves de tiempo.

Condiciones de reproducibilidad: condiciones en las cuales los resultados de una prueba se obtienen con el mismo método aplicado a idénticos objetos de prueba por diferentes operadores en diferentes laboratorios con diferentes equipos.

Condiciones de precisión intermedia: condiciones bajo las cuales los resultados de las pruebas se obtienen con el mismo método de prueba utilizando unidades de prueba o muestras tomadas al azar de una única cantidad de material que es tan homogénea como sea posible y con condiciones cambiantes como el operador, el equipo de medición, la ubicación dentro del laboratorio y el tiempo.

Las condiciones especificadas dan lugar a diferentes tipos de desviaciones estándar y precisiones con nombres correspondientes.

Por lo general, es cierto que la precisión de repetibilidad (r) es mayor que la precisión intermedia (I), que es a su vez mayor que la precisión de reproducibilidad (R). Sin embargo, por mal desempeño de los laboratorios, la precisión intermedia estimada, o incluso la precisión de repetibilidad estimada, puede ser peor que la reproducibilidad declarada por un estudio entre laboratorios para un método de prueba dado.
Para la desviación estándar, ya que tiene una relación inversa con la precisión, las relaciones se dan para el lado contrario:

σr < σ1 < σR

De hecho, pasar de las condiciones de repetibilidad a las condiciones intermedias y a las condiciones de reproducibilidad resulta en una complejidad adicional y las fuentes de variación que se agregan en cada paso, es decir, las condiciones de repetibilidad, tienen menos fuentes de variación de causa común que las condiciones intermedias, que son menos que las de las condiciones de reproducibilidad. En el contexto de las pruebas, la variación de causa común es un componente importante de los errores de medición. Las desviaciones estándar de repetibilidad y reproducibilidad se estiman como parte de un estudio entre laboratorios, como se describe en E691, Método para Llevar a Cabo un Estudio entre Laboratorios para Determinar la Precisión de un Método de Prueba.

La repetibilidad específica de laboratorio y las desviaciones estándar intermedias se pueden determinar mediante experimentos planificados o por análisis de rutina y el control de gráficos de muestras de control de calidad (E2554). La sigma del proceso estimada para un gráfico de control basado en mediciones repetidas de una muestra de control de calidad se determina normalmente en condiciones de precisión dentro del laboratorio.

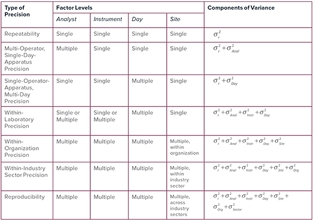
En el contexto de múltiples laboratorios dentro de una división o corporación, la precisión dentro de la organización, es importante que haya una forma de precisión entre laboratorios que sea más estrecha en su alcance que la reproducibilidad. La desviación estándar dentro de la organización se utiliza para establecer los límites de los programas internos de pruebas de aptitud. Las condiciones y fórmulas especificadas para las desviaciones estándar (de la población) asociadas con la repetibilidad, varios tipos de precisión y reproducibilidad intermedia, se resumen en la Tabla 1 a continuación. Mientras el alcance de la precisión se expande, los componentes de los términos de varianza deben entenderse como promedios de dominios cada vez más amplios. Como se mencionó anteriormente, la desviación estándar de repetibilidad estimada para un laboratorio individual puede ser muy diferente de lo que se publica en el método.

Tabla 1 — Descripción de los Tipos de Precisión

La Dependencia de la Precisión en la Matriz de la Muestra

La precisión de repetibilidad a menudo varía considerablemente por la matriz de la muestra. En general, las matrices más complejas tienen menor precisión de repetibilidad. Por ejemplo, la precisión de las pruebas del agua potable tenderá a ser mayor que la del agua de superficies naturales, que a su vez tenderá a ser más alta que la de las aguas residuales. Esto hace que sea muy aconsejable registrar las diferentes matrices en gráficos de control separados.

Cuando se trata de pruebas repetidas de una muestra de rutina, en lugar de un material de muestra de control homogeneizado, la precisión de los resultados depende en gran medida del grado de heterogeneidad de la muestra.

Dependencia de la Precisión de la Concentración de Analitos

Una característica universal de los datos derivados de las mediciones de química analítica es la varianza de error no constante. La desviación estándar de error en la química analítica se ha demostrado^1,2 que es razonablemente aproximada por una ley de potencia en un amplio rango (seis órdenes de magnitud) de concentraciones. Esto se ha demostrado en los datos de miles de ensayos en colaboración que involucran todas las tecnologías y matrices analíticas que se encuentran en los análisis de alimentos, de productos farmacéuticos y ambientales.

Sobre la base de un gran conjunto de ensayos en colaboración, cada uno con suficientes datos para estimar el exponente de la ley de potencia, las estimaciones de su valor tienden a estar cerca del 0.85.³ Por lo tanto, la desviación estándar del error en química analítica tiende a ser una función creciente de concentración que aumenta más lentamente que lo que indicaría un coeficiente de variación constante. Como consecuencia de esto, las muestras de control que tienen diferentes concentraciones deben registrarse en gráficos separados.

Hay, sin embargo, casos en los que el rango de concentración esperado para una aplicación específica de un método analítico es lo suficientemente estrecho para que la desviación estándar de error constante pueda ser una aproximación útil. No obstante, incluso a una concentración fija, una modificación menor de algo tan simple como la preparación de muestras puede cambiar la varianza del error. La varianza del error constante no debe suponerse sino más bien demostrarse a lo largo del rango de datos esperado por medio de una prueba F (u otra prueba estadística) comparando la varianza del rango esperado de las repeticiones del extremo inferior de la aplicación con la varianza de las repeticiones del extremo superior.

Referencias
1. Horwitz, W., Kamps L.R., Boyer K.W., Quality assurance in the analysis of foods and trace constituents. Journal of the Association of Official Analytical Chemists, Vol. 63, No. 6, 1980, pp. 1344-1354.
2. Horwitz, W., “Evaluation of analytical methods used for regulation of foods and drugs,” Analytical Chemistry, Vol. 54, 1982, pp. 67A-76A.

3. Thompson, M., “The Amazing Horwitz Function,” AMC Technical Brief No.17, Royal Society of Chemistry, 2004.