Preguntas sobre el tamaño de la muestra

Qué es grande

Por Thomas J. Bzik

P. ¿Es 30 un tamaño de muestra grande?

R. Tal vez.

Los textos estadísticos básicos a menudo describen 30 como el punto de partida para un tamaño de muestra grande. Grande es un descriptor impreciso. El concepto de grande necesita comprenderse, a menudo, en contextos no establecidos, antes de que sea posible decir que un determinado tamaño de muestra es grande. En nuestra breve travesía estadística, nos daremos cuenta de que a veces 30 es grande y a veces no. Por "grande" se entenderá lo suficientemente grande con respecto a un contexto de uso estadístico específico (a menudo la estimación de parámetros, como la media o la desviación estándar). Grande en un contexto estadístico significa, de manera burda, lo suficientemente grande como para proporcionar un resultado útil.

Los consejos sobre el tamaño de la muestra no difieren de otros consejos en que los consumidores prefieren una respuesta simple de "talla única para todos". Cuando se da una respuesta tentativa de, digamos, 30, bajo circunstancias específicas, gradualmente se transmuta en un consejo universal sobre el tamaño de la muestra. Este es un componente de la psicología del asesoramiento. La interpretación del consejo se vuelve más generalizada después de que el asesor deja de estar presente.

La mayoría de las situaciones en las que 30 se declara, estadísticamente, como suficientemente grande, normalmente implican estar, prácticamente, lo suficientemente cerca de una supuesta distribución normal asintótica. A continuación, información sobre un resumen de las sospechas habituales:

1. Punto de transición del tamaño de la muestra sugerido con frecuencia a partir del uso de la teoría de la muestra normal pequeña de t estadísticas hasta las Z estadísticas de muestra grande.

2. En los gráficos de control, se juzgan normalmente 30 puntos como suficientemente grandes para la estimación del límite de control en la construcción de gráficos de control basados en la supuesta normalidad de la distribución dentro de control.

3. El teorema del límite central implica que la distribución de cualquier promedio de la muestra de cualquier distribución con varianza finita se aproxima asintóticamente a la normalidad conforme n aumenta. A menudo, se supone que 30 es un tamaño de muestra suficientemente grande para que este resultado sea aplicable de manera práctica.

4. La distribución normal se ha utilizado para aproximar probabilidades binomiales donde
np > 5 y n(1-p) > 5. Esto implicaría que n = 30 es lo suficientemente grande para 1/6 < p < 5/6.

Afortunadamente, el asesoramiento con respecto a lo que constituye un tamaño de muestra grande se ha vuelto gradualmente más sofisticado en los textos estadísticos básicos durante las últimas décadas, y se han encontrado más calificaciones en las declaraciones sobre el tamaño de la muestra. Además, normalmente se proporcionan ecuaciones para estimar los requisitos de tamaño de la muestra para obtener estimaciones de parámetros que apuntan a un nivel de confiabilidad establecido. Si bien dichas estimaciones del tamaño de la muestra son muy útiles, no son el foco principal de la discusión actual.

Muchos de los principios de que 30 es suficientemente grande se originan en la era anterior a la computadora, en la que obtener una respuesta más exacta implicaba cálculos complejos. Treinta (30) fue el tamaño de la muestra en el que se consideró que muchas aproximaciones se habían vuelto suficientemente confiables. Las prácticas informáticas modernas de cálculo del tamaño de las muestras han cambiado gradualmente con respecto a 1; ahora una t-estadística se utiliza a menudo más allá de n = 30, pero no han cambiado casi nada con respecto al tamaño de la muestra en los gráficos de control.

¿Cuándo se vuelve problemáticamente pequeño un tamaño de muestra de 30 en los contextos 2 y 3? Los datos que no son normales pueden ser problemáticos, pero ¿cuándo? Para los gráficos de control construidos asumiendo la teoría normal, solo se puede tolerar desviaciones relativamente pequeñas de la normalidad antes de que la interpretación de los límites de los gráficos se altere de forma significativa. Aquí, un mayor tamaño de la muestra puede proporcionar una mejor comprensión de la forma de la distribución subyacente, pero no hará que los límites de control de la teoría normal sean representativos, independientemente del tamaño de la muestra que se obtenga. El teorema del límite central no se aplica a los límites de control estimados para observaciones individuales.

Figura 1: Ejemplos de distribuciones con sesgo.

El teorema del límite central funciona, pero hay una sutileza en cómo funciona con respecto al tamaño de la muestra. La velocidad, en términos de tamaño de la muestra, con la que la distribución del promedio de la muestra se aproxima a la normalidad es tanto una función del tamaño de la muestra como de la forma de distribución de los datos. Treinta (30) es lo suficientemente grande para algunas formas de distribución, pero no para otras. ¿Cuándo es 30 suficientemente bueno, o más que suficientemente bueno, para que el teorema del límite central funcione? Cuando la distribución de datos está distribuida simétricamente, o aproximadamente simétrica, y los datos no son excesivamente discretos.

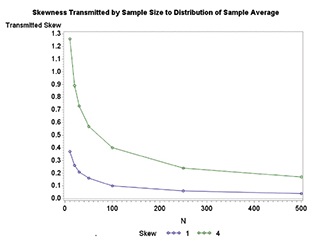
Figura 2: Transferencia de la asimetría a la distribución del promedio de la muestra en función del tamaño de la muestra.

Una medida estadística que normalmente identificará la asimetría es el sesgo (el tercer momento de una distribución después de la media y la desviación estándar). ¿Qué impacto tiene la asimetría en el hecho de que 30 sea un tamaño de muestra grande en el contexto del límite central? ¿Poco? ¿Mucho? Solo vale la pena discutir si se trata de esto último.

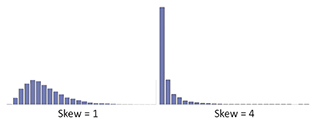
Considere la Figura 1, que ilustra dos niveles de sesgo de la población (sesgo = 1, sesgo = 4).

La asimetría afecta el teorema del límite central de dos maneras que disminuyen la tasa de convergencia de la distribución del promedio de la muestra a la normalidad:

1. Una distribución sesgada transfiere algo de sesgo a la distribución del promedio de la muestra (Figura 2).

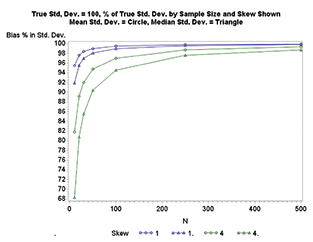
2. Las desviaciones estándar de la muestra están mucho más sesgadas hacia valores bajos en presencia de asimetría (Figura 3).

Figura 3: Sesgo en la estimación de la desviación estándar en función del tamaño de la muestra.

Considere dos ejemplos del impacto aproximado del sesgo en el teorema del límite central, por lo que se denominará tamaño efectivo de la muestra comparativa:

1. Sesgo ≈ 1: uso de N ≈ 30 implica un tamaño efectivo de muestra comparativa de N ≈ 20;

2. Sesgo ≈ 4: use of N ≈ 100 implica un tamaño efectivo de muestra de N ≈ 10.

La implicación del sesgo ≈ 1 es que uno podría estar dispuesto a considerar N = 30 aceptablemente grande para la aplicación del teorema

del límite central cuando |sesgo|≤ 1. Conforme |sesgo| se aproxima a 1, N = 50 es más seguro.

La implicación del sesgo ≈ 4 es que incluso N = 100 es un tamaño de muestra extremadamente insuficiente, ya que |sesgo| se aproxima a 4. Para obtener un tamaño de muestra efectivo de N = 30 para la aplicación del límite central con |sesgo| = 4, se requiere, aproximadamente, N = 500.

Nuestra breve travesía por el tema del tamaño de la muestra nos lleva a la pregunta fundamental:

¿Es 30 un tamaño de muestra grande? Tal vez siga siendo la respuesta, pero ahora sabemos mucho más acerca de cuándo 30 es grande y cuándo no lo es en varios contextos de tamaño de muestra.

Thomas J. Bzik es el actual presidente del Comité de Calidad y Estadística (E11). Representante de la Asociación Estadounidense de Estadísticas ante el Comité E11, también preside el subcomité de Muestreos/Estadísticas (E11.10).

John Carson, Ph.D., estadístico sénior de Neptune and Co., es el coordinador de la columna Data Points. Es presidente del subcomité sobre Control de calidad estadístico (E11.30), miembro del Comité de Calidad y Estadísticas (E11) y miembro de los Comités de Productos a base de petróleo, combustibles líquidos y lubricantes (D02), Calidad del aire (D22), Cannabis (D37) y Evaluación ambiental, gestión de riesgos y acción correctiva (E50).