Standardization News:

P.: ¿De qué probabilidad es el valor p?

R.: El valor p es un método breve comúnmente utilizado para informar los resultados de una prueba de hipótesis estadística, como en "El efecto es significativo (p = 0.013)". El citar el valor p proporciona más información que la afirmación simple de que la hipótesis nula de la prueba se rechaza o no se rechaza.

La práctica estándar para el cálculo y el uso de estadísticas básicas (E2586) agregó en 2018 una sección que describe brevemente los conceptos de pruebas de hipótesis y los términos asociados con estas, incluido el valor p¹. La definición dada para el valor p como término es: la probabilidad de observar una estadística de prueba al menos tan extrema como lo que se obtuvo realmente, bajo la suposición de la hipótesis nula.

En 2016, un comité especial de la Asociación Estadounidense de Estadística (American Statistical Association) emitió una declaración sobre los valores p. La ocasión para la declaración y parte de su contenido se tratará más adelante, pero la siguiente respuesta a nuestra pregunta está en la introducción a la declaración²: “Informalmente, un valor p es la probabilidad, según un modelo estadístico especificado, de que un resumen estadístico de los datos (por ejemplo, la diferencia media muestral entre dos grupos comparados) sea igual o mayor que su valor observado”.

Las pruebas de hipótesis son una parte importante del análisis estadístico. Se utilizan para afirmar que una variable X tiene efecto sobre otra Y. Esto se consigue estableciendo, como hipótesis nula, que X no tiene efecto sobre Y. Luego se diseña una estadística de prueba que sea sensible al efecto. Se elige un nivel de significación. Si la estadística de prueba está en una región crítica que se compone de los valores más probables en el caso de que X tenga un efecto sobre Y, se dice que la hipótesis nula está "rechazada". Otros usos de las pruebas de hipótesis son las pruebas para valores atípicos y pruebas de cumplimiento de suposiciones, como que una muestra viene de una distribución normal, hechas como parte del análisis de datos previo a las pruebas o la estimación de los efectos de la variable.

El valor p está relacionado con el nivel de significación de una prueba. Para evaluar una prueba de hipótesis, primero se elige una estadística de prueba con una distribución conocida según la hipótesis nula. Se diseñan estadísticas de prueba para medir la desviación de los datos respecto a la hipótesis nula en la dirección en que estamos interesados. Luego se ajustan las estadísticas de prueba de manera que sus distribuciones sean conocidas y, de ese modo, tabuladas. Algunos ejemplos son la estadística z:

y la estadística t de Student:

para probar una hipótesis acerca de una media, H₀: μ=μ₀. La normalización por σ/√n o por s/√n nos permite comparar la estadística utilizando una única tabla, independientemente de la desviación estándar (σ o s) y la cantidad de observaciones.

Origen del valor p y niveles de significación estándar para las pruebas de hipótesis

Conviene conocer algunos antecedentes históricos. El valor p precede al concepto de pruebas de significación o pruebas de hipótesis. La historia también muestra el origen de los niveles de significación que se usan con mayor frecuencia en las pruebas de hipótesis.

La aplicación que introdujo el valor p fue la de evaluación de la calidad del ajuste de una curva de graduación (curva de Pearson) a un conjunto de datos³. El criterio se llamó "bondad del ajuste". Al ajustar una curva a una distribución de datos, se seleccionó una forma de ecuación de distribución. Se estimaron los parámetros de la curva. Se agruparon los datos, y se comparó la cantidad de observaciones (O_i) en cada grupo con la cantidad esperada (E_i).

La estadística chi cuadrado:

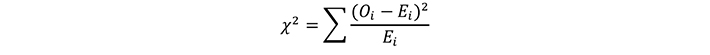
evaluaba la bondad de ajuste de los datos a la curva graduada. Para grandes cantidades de observaciones, la estadística tiene una distribución chi cuadrado. Una tabla de la distribución chi cuadrado da la probabilidad de que el valor calculado sea igualado o superado al azar como función de la cantidad de grupos. (Esto fue antes de que se conociera la reducción de grados de libertad debida a los parámetros ajustados). Este fue el valor p. Un valor bajo indicaría un ajuste defectuoso de la distribución a los datos. Un valor alto, cercano a 1, era igualmente sospechoso, ya que indicaría un sobreajuste a los datos de muestra.

Para una distribución única, como la normal estándar para la prueba z, todavía se da la función de distribución completa, probabilidad como función del valor de la variable, en los libros de texto y los libros de tablas matemáticas y estadísticas. La distribución chi cuadrado, y después la distribución t de Student para las pruebas de medias, diferencias y coeficientes de regresión, todas requieren tabulación para una serie de grados de libertad. Esto origina una tabla extensa y complicada de usar. Además, cuando Fisher escribió su texto clásico⁴ se le impidió, por derechos de autor, la reproducción de la tabla, bastante compacta, de la distribución chi cuadrado dada por Elderton. Por eso, se proporcionó un nuevo formato para la tabla. En lugar de dar la probabilidad acumulativa para un rango de valores de la estadística para cada grado de libertad, da percentiles seleccionados de la distribución para cada grado de libertad. Los percentiles incluidos en la tabulación fueron 0.05, 0.01 y posteriormente 0.001. Estos, por lo tanto, se convirtieron en los estándares para declarar los resultados de prueba significativos, altamente significativos y excesivamente significativos.

El proceso utilizado al efectuar pruebas de hipótesis, en la década de 1970, era calcular la estadística de prueba para los datos disponibles, y luego comparar el valor calculado con el percentil tabulado de la distribución en un libro de tablas para determinar la significación estadística.

Se introduce la computadora digital. Al efectuar los análisis estadísticos con computadoras y software, ahora es más fácil escribir una subrutina para calcular la distribución acumulativa que llevar una tabla de percentiles en la memoria, y la longitud de la tabla ya no es más un problema. Así, el valor p volvió a ser una forma preferida para informar los resultados de la prueba.

Los valores p se vuelven controversiales

En años recientes, el valor p se ha vuelto controversial en la ciencia. En investigación médica y en otras áreas, se comprueba que, con frecuencia, los intentos de replicar estudios publicados no obtienen el mismo efecto. Ionannidis señaló en un artículo influyente, titulado provocativamente,⁵ el modo en que muchos resultados de investigaciones médicas que se basan en pruebas de significación estadística no se confirman en estudios de seguimiento, si se publicaran. La Asociación Estadounidense de Estadística (American Statistical Association) respondió a las inquietudes con el desarrollo de su declaración. Un resumen altamente legible de los temas se encuentra en un informe de la Asociación Nacional de Académicos (National Association of Scholars) de los EE. UU.⁶.

No es tanto culpa del valor p en sí sino de la manera en la que se aplican erróneamente las pruebas de hipótesis en publicaciones científicas. Siempre se ha sabido de la necesidad de conocer las limitaciones de las técnicas, cosas que se deben tener presentes al realizar un análisis estadístico. Lo que causa problemas es la facilidad de realizar análisis estadísticos sin conocer estas limitaciones. Durante la redacción y la aprobación de la sección sobre pruebas de hipótesis de E2586, los autores estaban muy conscientes de las cuestiones acerca del mal uso y la interpretación errónea, por lo que agregaron en ese estándar notas de clarificación y advertencias.

Algunas de estas cuestiones son las siguientes:

• El valor p no puede interpretarse en ningún sentido como una probabilidad de que la hipótesis nula sea verdadera. Aunque es una medida válida para indicar hasta qué punto un conjunto de datos es incompatible con la hipótesis, esa medida no es interpretable como una probabilidad. La probabilidad de la hipótesis nula, dados los datos, puede evaluarse en un marco bayesiano, dadas las probabilidades previas de las hipótesis nula y alternativas. La probabilidad de una hipótesis nula que es rechazada por una prueba estadística será menor que si no es rechazada. Sin embargo, la probabilidad de la hipótesis nula no está dada por el valor p.

• La significación estadística indicada por el valor p no mide la importancia práctica de un efecto. Además, el rechazo en una prueba de la hipótesis nula no es evidencia definitiva para ninguna alternativa particular.

• Cuando se efectúan muchas comparaciones estadísticas sobre un conjunto de datos, y principalmente se informan y usan para basar conclusiones aquellas que son estadísticamente significativas, el nivel de significación nominal para las pruebas ya no se aplica, y las conclusiones deben considerarse especulativas.

• La presentación de informes selectiva, en la que los datos se informan solo cuando la prueba estadística es significativa, es un grave problema que puede distorsionar el proceso científico y comprometer la validez de las conclusiones. La solución a este problema es la disciplina en la formulación de las hipótesis a probar y las expectativas de los resultados a obtener antes de recolectar los datos, y la presentación de informes completa cualesquiera sean los resultados de la prueba. 

Referencias
1. The Standard Practice for Calculating and Using Basic Statistics (E2586).
2. L. Wasserstein and N. A. Lazar, “The ASA’s Statement on p-values: Context, Process, and Purpose,” The American Statistician, Vol. 70, No. 2, May 2016, pp. 129-133.
3. W. P. Elderton, Frequency Curves and Correlation, 4th ed., Cambridge University Press, 1953 (1^st ed. 1906).
4. A. Fisher, Statistical Methods for Research Workers, 14th ed., Hafner, 1970 (1^st ed. 1925).
5. P. A. Ioannidis, “Why Most Published Research Findings Are False,” PLoS Medicine, Vol. 2, No. 8, August 2005, E124.
6. Randall and C. Welser, The Irreproducibility Crisis of Modern Science, National Association of Scholars, April 2018.