Standardization News:

P. ¿Cómo ayuda contar con un modelo estadístico de Weibull en la planificación de pruebas de confiabilidad?

R. En nuestro primer artículo sobre este tema, comentamos cómo funciona un plan de pruebas, los parámetros de prueba, el tipo de datos que se obtienen y ciertos casos que se denominan no paramétricos en cuanto a que no dependen de una distribución asumida para el modo de fallo¹. En esta parte, ampliamos estos conceptos y agregamos la suposición de un modelo estadístico de Weibull para el modo de fallo subyacente.

La distribución de Weibull es un modelo de amplio uso para los fenómenos de fallo en pruebas de materiales, sistemas y componentes electromecánicos. Es capaz de modelar las tres clasificaciones más importantes de los modos de fallo que suelen encontrarse: a) fallas aleatorias, b) fallas por desgaste o degradación, y c) fallas tempranas denominadas “mortalidad precoz”. Asimismo, estas tres clasificaciones están relacionadas con valores específicos del parámetro de forma de la distribución de Weibull, β. Cuando las fallas son aleatorias, β = 1; cuando las fallas están relacionadas con un desgaste o degradación, β > 1; y cuando las fallas están relacionadas con la mortalidad precoz, β < 1.

Con frecuencia, el punto de partida para la demostración de los requisitos de confiabilidad es suponer que b = 1. En el caso de los tipos de modo de fallo por desgaste/fatiga, comúnmente se encuentra que 1 < β ≤ 4. Durante la presentación o el lanzamiento temprano de un producto o después de realizar algunas modificaciones al producto, por lo general, se usa β < 1. En líneas generales, no realizamos pruebas para el caso de la mortalidad precoz, aunque es posible en teoría, ya que los valores más pequeños de β suelen implicar una mayor variación en la vida útil de un producto.

Al momento de diseñar un plan de pruebas para el caso del modelo de Weibull, tenemos que suponer un valor de β. En general, podría haber un buen motivo para cualquiera de las opciones, ya que podrían existir datos (antecedentes) para extraer dentro de una determinada empresa o podría haber cierto reconocimiento del dominio público de una variedad de posibles valores de β dentro de una industria o sector determinado para un tipo de modo de fallo en particular.

El modelo estándar de Weibull de dos parámetros tiene una función de distribución acumulativa de forma cerrada que se describe como:

(1)

En la ecuación 1, F(t) es la probabilidad de falla acumulada en el tiempo t; β es el parámetro de la forma de Weibull (también denominado la pendiente de Weibull) antes mencionado; y η es la vida característica de Weibull, o el percentil 63,2 del modelo de distribución de Weibull. La ecuación 1 se utiliza, junto con otra teoría, en el desarrollo de planes de pruebas para el modelo de Weibull.

Planificación de demostración de confiabilidad: Modelo de Weibull de cero fallas

Si recordamos que, si se prueban n unidades por un tiempo t y no se producen fallas, si utilizamos la confianza C, el requisito del tamaño de muestra para demostrar una confiabilidad, R, sería:

(2)

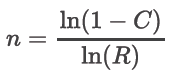
Si la distribución de Weibull es una suposición, la ecuación 2 se modifica según se muestra en la ecuación 3:

(3)

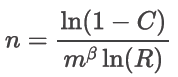
En la ecuación 3, la variable m es la relación entre el tiempo de prueba t y el tiempo y en el que se aplica la confiabilidad R. Es la “cantidad de vidas” a la que equivale el tiempo de prueba t, donde una “vida” es la vida que tiene una confiabilidad R. El parámetro de forma (pendiente) supuesta de Weibull también es necesario. La ecuación 3 proviene del hecho de que no está permitido que se produzcan fallas y utiliza la relación no paramétrica fundamental entre la confiabilidad, la confianza y el tamaño de la muestra, de modo que Rⁿ . Luego, la sustitución de la función de confiabilidad de Weibull con R(y) junto con cierta álgebra da como resultado la ecuación 3 (véase la referencia 2 para obtener más detalles).

Por ejemplo, si queremos demostrar una confiabilidad R del 90 % a y = 1000 ciclos con una confianza C del 90 %, usar una ecuación 2 sin una suposición de Weibull da como resultado un tamaño de muestra n de 22 unidades comprobadas a t = 1000 ciclos sin fallas. Imagine que suponemos una distribución de Weibull para el modo de fallo, suponemos un mecanismo de desgaste modesto con un valor β de Weibull de 2, y estamos dispuestos a realizar pruebas por el doble de tiempo (t = 2000 ciclos), m =t/y = 2000/1000 = 2, y usar la ecuación 3 genera un nuevo tamaño de muestra n de 5,46 o 6. Fundamentalmente, esto indica que la suposición de Weibull con β = 2 y el doble del tiempo de prueba (2000) demostrará una confiabilidad a 1000 ciclos con una disminución del tamaño de la muestra a una cuarta parte. Por supuesto, debemos poner a prueba la cantidad de unidades más pequeña por un período más largo de modo que exista un creciente riesgo de falla usando el tiempo más prolongado.

Una primera variación de esto es el caso en el que un tamaño de muestra ha avanzado sin fallos a lo largo de una prueba, pero los tiempos de prueba son variables. Entonces, con el tamaño de prueba n, los tiempos variables t_i y la confianza C, podemos determinar la confiabilidad demostrada en el tiempo arbitrario y, R(y). La ecuación que rige este caso es la ecuación 4:

(4)

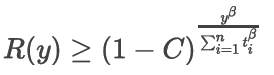
La ecuación 4 se puede reorganizar para mostrar la vida demostrada en función de una confiabilidad R específica. A esto se le denomina “vida B_p”, donde p es un porcentaje y B_p es la vida en la que hay una confiabilidad del (100 - p) %. Por ejemplo, la vida B₁₀ es la vida en la que hay una confiabilidad del 90 %. Esta versión con cero fallas, confianza C, valor β de Weibull supuesto y tiempos variables se expresa de la siguiente manera:

(5)

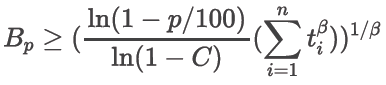
Ahora, suponga que hay seis tiempos de prueba y cada uno de ellos ha avanzado por una cantidad variable de ciclos en pruebas sin fallas. Considere que los valores de prueba son {250, 380, 428, 750, 618, 663} y suponga que la distribución de Weibull se aplica con β = 2. Dada una confianza del 90 %, ¿cuál es la confiabilidad demostrada a y = 275 ciclos? Con la ecuación 4, encuentre que el exponente es 0,04263, que brinda una confiabilidad a y = 275 ciclos de 0,907 o alrededor del 91 %. ¿Qué vida B₅₀ se demuestra usando estos datos? Con la ecuación 5, B₅₀≥ 730,8 con una confianza del 90 %.

La tabla 1 muestra los requisitos del tamaño de muestra para diversos valores de m y el valor β de Weibull usando la nomenclatura “RC” (confiabilidad-confianza). Por ejemplo, R90C95 significa un requisito de confiabilidad del 90 % y una confianza del 95 %. Para ilustrar su uso, suponga un requisito de confiabilidad de R = 95 % a y = 1500 ciclos usando una confianza del 90 % (R95C90). Si se supone un valor β de Weibull de 3 y si podemos probar cada elemento por m = 2 veces el requisito (es decir, 2*1500=3000), la tabla 1 muestra que el tamaño de muestra n es 5,6 o 6 unidades (redondeado hacia arriba).

Tabla 1: Requisito del tamaño de muestra; planes de Weibull de cero fallos; confiabilidad y confianza especificadas con la nomenclatura “RC”¹

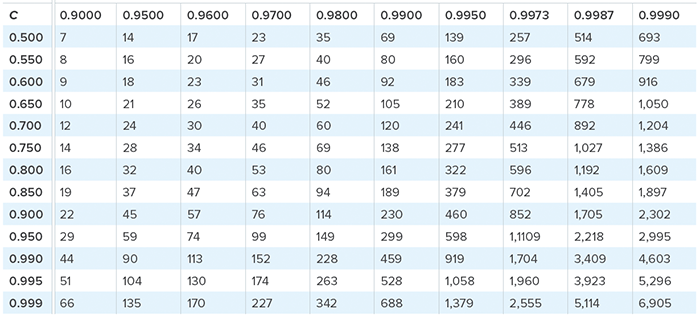
1. El valor m es la relación entre el tiempo de prueba, t, y el requisito de confiabilidad, y. La nomenclatura “RC” indica la “confiabilidad” y la “confianza” utilizadas.

Los especialistas deberían percatarse de que, al igual que los planes de cero fallas no paramétricos, los planes de cero fallas de suposición de Weibull son muy conservadores. Si simplemente cumplimos con el requisito establecido, incluidas las suposiciones, y usamos cierta confianza C (expresada como un número decimal), la probabilidad de aprobar alguna prueba es de 1 - C. Por lo tanto, con un plan de cero fallas, se espera que el material o componente que se prueba sea mejor que el requisito que hemos establecido para él.

En una futura edición de Data Points, continuaremos con el debate sobre la planificación de pruebas con un análisis de los planes de Weibull que admiten una o más fallas.

Referencias:

1. Luko, Stephen, y Neubauer, Dean, “Building on Reliability: Reliability Test Planning” (Reforzar el concepto de confiabilidad: Planificación de pruebas de confiabilidad), (Data Points), ASTM Standardization News, Vol. 49, N.º 1, enero/febrero de 2021, pág. 52-53.

2. Luko, Stephen, “Weibull Analysis with Assumed Weibull Slope Where NO Failures Are Observed” (Análisis de Weibull con pendiente de Weibull supuesta en el que NO se observan fallas), informe técnico de SAE 982032, International Off-Highway and Powerplant Congress and Exposition, Milwaukee, Wisconsin, del 14 al 16 de septiembre de 1998.

Stephen N. Luko es asociado y estadístico de United Technologies Corp/Collins Aerospace. Es presidente del subcomité sobre confiabilidad, integrante del comité sobre calidad y estadística (E11), miembro de ASTM International, ganador del premio Harold F. Dodge y expresidente del comité E11.

Dean V. Neubauer, ingeniero asociado y jefe de Estadística de Corning Inc., y coordinador de la columna Data Points, es vocal del subcomité ejecutivo del comité sobre calidad y estadística (E11), miembro de ASTM International y expresidente del comité E11.