Standardization News:

P: ¿Puedo inferir algo sobre una población o un proceso en función de una estimación puntual?

R: Es arriesgado utilizar una estimación puntual basada en una sola muestra de datos para inferir algo sobre una población o un proceso, ya que no tiene en cuenta las fuentes de variación inherente. Consideremos, por ejemplo, utilizar la media de la muestra como una estimación puntual de la media de la población. Si se extrajeran varias muestras de datos del mismo tamaño en las mismas condiciones de una población, las medias de la muestra resultantes serían todas diferentes porque los valores que componen cada muestra de datos serían diferentes. Esto ilustra la incertidumbre debida al muestreo. También puede haber otras fuentes de variabilidad, como las debidas a efectos medioambientales o a errores de medición.

Los intervalos estadísticos se emplean para tener en cuenta la incertidumbre en una estimación puntual sobre la base de una sola muestra de datos, que es la práctica común. Aunque los intervalos estadísticos se pueden aplicar en una amplia variedad de aplicaciones, es un tema que generalmente no se entiende bien.

P: ¿Puedo inferir algo sobre una población o un proceso en función de una estimación puntual?

R: Es arriesgado utilizar una estimación puntual basada en una sola muestra de datos para inferir algo sobre una población o un proceso, ya que no tiene en cuenta las fuentes de variación inherente. Consideremos, por ejemplo, utilizar la media de la muestra como una estimación puntual de la media de la población. Si se extrajeran varias muestras de datos del mismo tamaño en las mismas condiciones de una población, las medias de la muestra resultantes serían todas diferentes porque los valores que componen cada muestra de datos serían diferentes. Esto ilustra la incertidumbre debida al muestreo. También puede haber otras fuentes de variabilidad, como las debidas a efectos medioambientales o a errores de medición.

PARA USTED: Algunos puntos precisos para determinar la conformidad con la especificación – Data Points

Los intervalos estadísticos se emplean para tener en cuenta la incertidumbre en una estimación puntual sobre la base de una sola muestra de datos, que es la práctica común. Aunque los intervalos estadísticos se pueden aplicar en una amplia variedad de aplicaciones, es un tema que generalmente no se entiende bien.1 Este artículo combina información de entregas anteriores de Data Points para proporcionar una visión general de alto nivel de los tipos comunes de intervalos estadísticos, la selección de intervalos y ejemplos de formulación de intervalos.2

Los intervalos comunes en estadística son el intervalo de confianza (IC), el intervalo de predicción (IP) y el intervalo de tolerancia (IT). La selección del intervalo depende del propósito del intervalo y la estadística de interés.3 Un IC se usa para hacer una inferencia sobre un parámetro desconocido, como una media, una desviación estándar o una proporción. Un IP se utiliza cuando interesa predecir límites para una o más observaciones futuras. Un IT se emplea para captar una proporción específica de la población. Se pueden aplicar métodos paramétricos (con una distribución supuesta) y métodos no paramétricos (sin ninguna distribución) para formar cada tipo de intervalo. Los métodos paramétricos y no paramétricos suponen que la muestra es una representación aleatoria de una población o un proceso estables.4

Los intervalos estadísticos pueden ser unilaterales o bilaterales. Por ejemplo, un IC bilateral se utiliza generalmente cuando se hace una inferencia respecto de la media, mientras que un IC unilateral se emplea a menudo cuando se calcula la confiabilidad. Todos los intervalos tienen un nivel de confianza, que representa la creencia (como probabilidad porcentual) de que el método utilizado para crear el intervalo ha captado correctamente la verdad. El nivel de confianza se especifica de antemano para los métodos paramétricos, habitualmente, en 95 %. Para métodos no paramétricos es una función del tamaño de la muestra (y de la proporción para un IT).

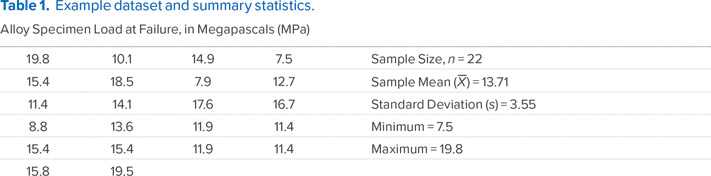
Los datos de la Tabla 1 se utilizan en la Tabla 2 para proporcionar ejemplos de IC, IP e IT bidireccionales que suponen una distribución normal y contrapartes de IP e IT no paramétricas.5

Para intervalos paramétricos, en general y como se observa en la Tabla 2, un IP siempre será más amplio que un IC para el mismo nivel de confianza y tamaño de la muestra. Observe que, con un tamaño de muestra de n = 22, los niveles de confianza para el IP y el IT no paramétricos son del 91 % y el 66 %, respectivamente.

Aunque no existe un método correcto único para crear un tipo dado de intervalo, es importante comprender las ventajas o las limitaciones de los métodos disponibles. Si no se mantiene la normalidad, un método no paramétrico puede ser la mejor opción. Sin embargo, se necesitaría, al menos, n = 39 y n = 46 para el IP y el IT no paramétricos, respectivamente, a fin de obtener un nivel de confianza equivalente del 95 % frente al tamaño de muestra de ejemplo de 22.

Para obtener la información más completa sobre intervalos estadísticos, se recomienda al lector consultar Statistical Intervals: A Guide for Practitioners and Researchers.6

REFERENCES

1  Luko, S.N. (Editor). Presentation of Data and Control Chart Analysis (“Manual 7”). Ninth Edition. ASTM International, 2018.
2   Luko, S.N. and Neubauer, D.V. “Statistical Intervals Part 1: The Confidence Interval.” Standardization News (July/Aug. 2011): 18-20; “Statistical Intervals Part 2: The Prediction Interval.” Standardization News (Sept./Oct. 2011): 14-15; “Statistical Intervals Part 3: More on the Tolerance Interval.” Standardization News (Nov./Dec. 2011): 18-19; “Statistical Intervals: Nonparametric Intervals Part 1.” Standardization News (Nov./Dec. 2013): 20-21; “Statistical Intervals: Nonparametric Intervals Part 2.” Standardization News (Jan./Feb. 2014): 20-21.
3   Luko, S.N. Presentation of Data and Control Chart Analysis.
4   Ibid.
5   Luko, S.N. and Neubauer, D.V. “Statistical Intervals Part 1: The Confidence Interval.”
6   Meeker, W.Q., Hahn, G.J., and Escobar, L.A., Statistical Intervals: A Guide for Practitioners and Researchers. Second Edition. John Wiley & Sons, Inc., 2017: (103-104).
7  Ibid.; Wilks, S.S. Mathematical Statistics. New York: John Wiley & Sons, 1962.