Puntos de datos: una introducción a la distribución de Poisson y aplicaciones en control de calidad y análisis de riesgos

Puntos de datos: una introducción a la distribución de Poisson y aplicaciones en control de calidad y análisis de riesgos
La distribución de Poisson es una de las distribuciones más importantes de toda la estadística. Es una distribución discreta y contabiliza determinados tipos de eventos en el tiempo o en algún otro tipo de intervalo observable, como el área, el volumen o la distancia. La distribución debe su nombre al matemático y físico francés Siméon Denis Poisson (1781-1840), que la describió en una obra temprana referente a la investigación sobre la probabilidad de los veredictos penales y civiles.1 Para derivar la distribución, Poisson utilizó un método basado en la forma límite de una distribución binomial cuando p se aproxima a 0. En general, este es el método que utiliza la mayoría de los libros de texto en la actualidad.2 Otros investigadores, posteriores a Poisson, han demostrado que se aplica a diversos fenómenos. Parte de esta historia fue resumida recientemente por Hanley y Bhatnagar.3
CARACTERIZACIÓN
La distribución de Poisson consiste en contar eventos aleatorios en un intervalo de observación fijo, como el tiempo, el área, el volumen, la longitud, etc. Puede ocurrir cualquier número de eventos en el intervalo (0≤X<∞). Este caso es distinto del de una distribución binomial, en la que hay un número fijo, n, de ensayos y se cuentan tanto los éxitos como los fracasos.4 La distribución de Poisson solo cuenta los eventos. Por ejemplo, podemos contar las piezas que faltan en una unidad de montaje compleja en un proceso de fabricación, la ocurrencia de picaduras en una superficie metálica de un metro cuadrado de un material o los accidentes en una intersección concurrida en hora pico. En cada caso, si un evento no ocurre, no se puede contabilizar. Un punto muy importante sobre el intervalo de observación es que debe ser homogéneo, lo que significa que los eventos que se produzcan en dos subregiones cualesquiera del intervalo que no se superpongan son independientes. Además, la probabilidad de cualquier número de eventos en dos subintervalos no superpuestos del mismo tamaño dentro de la región de observación debe ser idéntica. Así, si el intervalo que observamos es el tiempo entre las 7:00 y las 8:00 a. m., la probabilidad de un evento entre las 7:00 y las 7:05 es idéntica a la de un evento entre las 7:45 y las 7:50. Esta suposición debe pensarse detenidamente en cualquier aplicación ya que la falta de homogeneidad alterará el comportamiento probabilístico. Lo único que determina completamente el comportamiento probabilístico en el intervalo de observación es el número medio o esperado de eventos en el intervalo. La descripción de la homogeneidad implica además que la media es proporcional a la longitud/tamaño del intervalo mientras sigan prevaleciendo las condiciones de homogeneidad. Cabe señalar que no es necesario que la media sea un número entero, así que, por ejemplo, la media podría ser 3.25 o 0.367 eventos.
Para un intervalo de observación fijo, la media se denota como µ>0. La función de masa de probabilidad para la distribución de Poisson, y que rige los eventos en el intervalo, viene dada como:
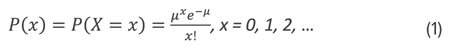
Una caracterización alternativa consiste en utilizar una constante de tasa, λ y un parámetro auxiliar t. La media en el intervalo de tamaño t se vuelve µ=λt. El parámetro de tasa λ incluye las unidades de eventos por unidad de tiempo (o área, volumen, longitud, etc.). Las unidades de λ y t deben ser las mismas. Por ejemplo, si λ fuera igual a 0.036 eventos por pulgada cuadrada, entonces en una región homogénea de t=144 pulgadas cuadradas, la media se calcularía como µ=λt=0.036(144)=5.184 eventos. Supongamos que en cambio deseamos estudiar una región de 40 pulgadas cuadradas. La media cambiaría proporcionalmente a (40/144)(5.184)=1.44 eventos en el nuevo intervalo de 40 pulgadas cuadradas. La forma de la distribución de Poisson que utiliza λ y t se encuentra a menudo en aplicaciones de análisis de riesgos.
APLICACIONES
Cuando se inventaron los diagramas de control a principios de la década de 1930, los investigadores se dieron cuenta rápidamente que se podían utilizar los datos de tipo atributo, y los datos variables, con los diagramas de control. El diagrama p, que se basa en la distribución binomial, es bien conocido. Lo que probablemente es menos conocido y probablemente subutilizado, es el diagrama c. Este traza eventos de tipo Poisson en un proceso. Existen numerosos tipos de estos eventos de tipo aleatorio en los procesos de fabricación, empresariales y de otros sectores. Algunos ejemplos son las imperfecciones de áreas superficiales, las picaduras o arañazos en las piezas metálicas, los componentes que faltan en un montaje complejo, las averías de los equipos en un turno de ocho horas, los errores en los dibujos o en los textos, las llamadas a un servicio de asistencia técnica para solicitar el mantenimiento de una computadora, los accidentes laborales trimestrales con tiempo perdido en una gran planta, las visitas a la página web en un día, los trabajos que hay que rehacer, la merma de mano de obra en una gran empresa y muchos otros. Para crear un diagrama c para una región de observación o un tamaño de muestra constantes, solo se necesita el número medio de eventos en una muestra inicial. Para la distribución de Poisson, sigma se calcula como la raíz cuadrada de la media. Así, si el número medio de manchas de material en un grupo de unidades de producto es 4, sigma es 2, lo que hace un límite de control superior “3 sigma” de 4+3(2)=10.
La distribución de Poisson se utiliza a menudo para hacer modelos de eventos “raros” o poco frecuentes como los que se encuentran en el análisis de riesgos. Tales eventos se encuentran por lo general en intervalos de tiempo y, en estos casos, existe una relación entre el número de eventos y el tiempo transcurrido entre ellos. La distribución del tiempo entre eventos cuando se observa un proceso de Poisson homogéneo se denomina distribución exponencial. La distribución de Poisson cuenta los eventos en un intervalo de tiempo y la exponencial mide el tiempo entre los eventos. La exponencial está completamente determinada por un único parámetro, θ, el tiempo medio entre los eventos. De nuevo, a menudo se utiliza una constante de tasa, λ=1/θ en su caracterización.
Utilizando la parametrización de la tasa, la función de densidad, f(t) y la función de distribución acumulativa, F(t), para la exponencial son:

La función R(t)=1-F(t)=exp(-λt) también se utiliza mucho en la práctica y se denomina fiabilidad en el tiempo t. La fiabilidad puede entenderse como la media de la probabilidad de supervivencia en el tiempo t. En (1), si utilizamos µ=λt como la parametrización de Poisson y x=0 para indicar 0 eventos en el intervalo t, entonces vemos que F(t), anterior, es su complemento, es decir la probabilidad de que se produzca al menos un evento en el tiempo t. En otras palabras, la probabilidad de que un evento tarde un tiempo t para que ocurra es igual a la probabilidad de Poisson de que ocurra al menos un evento en el tiempo t. Esto establece el vínculo entre las distribuciones de Poisson y la exponencial. La distribución exponencial tiene la curiosa propiedad “sin memoria” en el sentido de que dado que un evento no ha ocurrido en un tiempo t, la probabilidad de que un evento ocurra en un tiempo adicional s es idéntica a la probabilidad de que un evento inicial pueda ocurrir en un tiempo s. Así, el proceso no se ve afectado por el hecho de que transcurra el tiempo t sin un evento. Este es verdaderamente el factor clave de la forma en que se comportan los eventos aleatorios.
En la calidad de los productos, si un defecto o modo de fallo es un evento de tipo aleatorio, entonces dado el uso del producto durante cierto tiempo sin fallos, el producto se considera tan bueno como un objeto nuevo con respecto a dicho modo de fallo aleatorio. En el lenguaje de la fiabilidad esto también significa, cuando se trata de modos de fallo aleatorios, que R(s+t)=R(s)R(t). Se puede encontrar más información sobre la distribución exponencial en una publicación anterior de la columna Data Points.5
REFERENCIAS
1 Stigler, S. The History of Statistics: The Measurement of Uncertainty Before 1900. Cambridge, MA: Harvard University Press, 1986: 182.
2 E.g. Hogg, R. V. and Tanis, E. A. Probability and Statistical Inference. 7th edition. Saddle River, NJ: Prentice Hall, 2006.
3 Hanley, J. A. and Bhatnagar, S. “The ‘Poisson’ Distribution: History, Reenactments, Adaptations.” The American Statistician, Vol. 76, No. 4 (2022): 363-371.
4 Brown, J. and Dalton, C. “Quantifying Probability of Detection (POD) Using the Binomial Distribution.” Stadardization News (enero/febrero 2023): 50-51.
5 Luko, S. N. “What is Reliability: Key Concepts and Terminology.” Standardization News (enero/febrero 2018): 28-29.
Stephen N. Luko, antiguo miembro de Collins Aerospace Corporation, Windsor Locks, Connecticut, fue presidente del comité de calidad y estadística (E11) y es el actual presidente del subcomité de fiabilidad (E11.40), además de miembro de ASTM International.
El Dr. John Carson, de P&J Carson Consulting LLC, Findlay, Ohio, es el coordinador de la columna Data Points. Es presidente del subcomité de control de calidad estadística (E11.30), forma parte del comité de calidad y estadística (E11) y miembro del comité de evaluación medioambiental, gestión de riesgos y acciones correctivas (E50).