Uso de reglas de interpretación de gráficos de control

Descripción y estrategia

Por Polona K. Carson y John H. Carson Jr.

P: ¿Qué son las reglas de gráficos de control y qué reglas deben aplicarse a la interpretación de gráficos de control?

R: Los gráficos de control que se utilizan en las pruebas son herramientas estadísticas para detectar alteraciones en el proceso de prueba en términos de cambios en la ubicación del proceso/valor medio y variaciones en el proceso. El proceso de prueba es estable cuando los resultados de las mediciones son predecibles dado un valor conocido del mensurando, la variable que se mide. Esto implica que también se caracteriza la confiabilidad de la medición de incógnitas.

Un proceso que ha demostrado ser estable a través de los resultados de las pruebas de gráficos de control de muestras a través de una gama de medición puede esperarse que produzca mediciones de elementos de prueba desconocidos con un sesgo y una precisión comparables al rendimiento indicado por las muestras de control. Esto supone que los materiales de control son representativos de los elementos de prueba.

Los gráficos de control que se describen en la práctica para el uso de gráficos de control, en el control de procesos estadísticos (E2587), se basan en la suposición de que los datos del proceso son independientes y tienen una distribución normal. Los gráficos para ubicación del procesoy para las variaciones en el proceso (gráfico mR, gráfico R o gráfico S) son necesarios para una caracterización sólida de un proceso de prueba. Ambos tipos de gráficos se definen a través de parámetros similares:

• línea central, valor promedio de una media o variación de estimación estadística, y
• límites inferior y superior en torno a la línea central.

Las reglas de Western Electric (WE) descritas en E2587 están diseñadas para distinguir entre la variación de procesos naturales y la variación por causas especiales. Las más conocidas son las primeras cuatro reglas de WE:

• La regla de Shewhart: un valor cae fuera de cualquier límite de control tres sigma.
• Dos de tres valores consecutivos caen fuera de los límites de advertencia de dos sigma del mismo lado.
• Cuatro de cinco valores consecutivos caen fuera de los límites de advertencia de un sigma del mismo lado.
• Ocho valores consecutivos se encuentran por encima o debajo.
  Un gráfico de control indica cuando se infringe una de sus reglas de evaluación. La regla 1 es bastante sensible a una variación grande en el proceso (>2,5 sigma), pero tiene muy poca capacidad para detectar variaciones de <1,5 sigma dentro de un tiempo razonable. Las reglas 2 a 4 hacen que el gráfico de control sea más sensible a variaciones más pequeñas.

Todas las reglas (procedimientos de decisión) deben evaluarse en términos de cómo equilibran el riesgo entre el error de tipo I y el de tipo II. Un error de tipo I se produce cuando un gráfico indica por error que el proceso está fuera de control. Un error de tipo II se produce cuando un gráfico no indica que el proceso de prueba está fuera de control. La tasa de error de tipo II depende de las propiedades de la causa especial, la desviación con respecto al proceso del estado estable.

Suponiendo que el proceso es estable, que la desviación media y estándar se conocen perfectamente y que el proceso de prueba realmente sigue una distribución normal, la tasa de error de tipo I conforme a las reglas 1, 2, 3 y 4 es del 0,27, 0,20, 0,13 y 0,78 por ciento, respectivamente. Las reglas de WE suelen utilizarse en combinación, lo que puede aumentar considerablemente la tasa de error de tipo I acumulada.

Otro aspecto importante del comportamiento del gráfico es la distribución de las longitudes de secuencia (RL). Una secuencia se refiere a la secuencia de puntos entre eventos cuando el gráfico está indicando. En el caso anterior, estimamos en promedio una señal falsa positiva por 370 puntos conforme a la regla 1, una longitud de secuencia promedio en control (ARL) de 370.

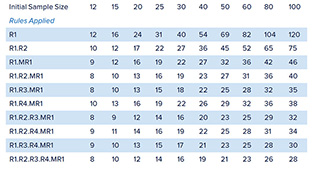
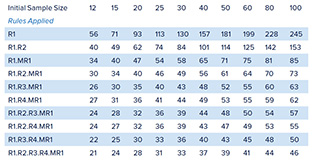
En la práctica, los parámetros de proceso no se conocen, sino que se estiman. La tasa de error de tipo I de todas las reglas de WE aumenta considerablemente en este caso a menos que la cantidad de datos utilizados para estimar los parámetros de proceso sea bastante grande. Para examinar las tasas falsas positivas de señalización de gráficos de control para un gráfico I/MR con varias reglas de WE aplicadas, simulamos usar diferentes tamaños de muestras iniciales para estimar los parámetros del gráfico y utilizamos diferentes combinaciones de las primeras cuatro reglas de WE en combinación con la regla 1 aplicada al gráfico MR (MR1). La simulación aplicó las reglas solas y en diversas combinaciones a 32 000 secuencias de valores con distribución normal independiente, cada secuencia de una longitud de 5000. Los resultados para la ARL en control y la RL mediana se muestran en las tablas 1 y 2. Las longitudes de secuencia se estimarían por encima de la RL mediana la mitad de las veces.

Tabla 1— ARL en control para gráfico I/MR.

Las entradas “Reglas aplicadas” se interpretan, por ejemplo, R1.R2.MR1 significa aplicar las reglas 1 y 2 de WE con MR1.

La distribución de las longitudes de secuencia está demasiado sesgada a la derecha. Por lo tanto, los valores de la RL mediana en la tabla 2 son considerablemente más pequeños que los valores ARL de la tabla 1, que están inflados debido a algunas longitudes de secuencias muy largas, especialmente en los casos en que la desviación estándar del proceso está demasiado sobrestimada. La RL mediana está mucho más cerca de la sensación intuitiva que el usuario de un gráfico de control tendría al pensar sobre la longitud de la secuencia.

Tabla 2 — RL mediana en control para gráfico I/MR.

Recomendación

Como se demostró anteriormente, debemos tener cautela al utilizar reglas de interpretación, ya que debemos evitar demasiadas señales falsas positivas en los gráficos de control. Recomendamos la siguiente estrategia.

Comience aplicando la regla 1 de WE al gráfico de control para monitorear el valor medio y MR1 para interpretar el gráfico en cuanto a variaciones. Esto indicará rápidamente perturbaciones grandes (>2,5 sigma) en el proceso de prueba que pueden ser catastróficas para la calidad de los datos de laboratorio. Una vez que el gráfico de control no muestre evidencia de inestabilidad del proceso, pueden agregarse más reglas de WE para aumentar la sensibilidad del gráfico a perturbaciones más pequeñas en el proceso de prueba.

No obstante, una mejor estrategia es utilizar un gráfico EWMA (promedio móvil exponencialmente ponderado) o CUSUM (suma acumulada) como complemento, según se describe en el artículo sobre puntos de datos anterior, Gráficos de control para monitorear el rendimiento del método de prueba (SN, marzo/abril de 2016) para monitorear el proceso para detectar cambios medianos y pequeños (<1,5 sigma).

Actualizar los parámetros del gráfico a medida que se agregan más puntos también ayudará considerablemente en cualquiera de los dos casos.

En un próximo artículo, presentaremos algunos resultados sobre la capacidad de los gráficos de control para detectar variaciones en los procesos y compararemos las reglas de WE con gráficos complementarios en términos de su ARL y RL mediana.

Polona K. Carson, Ph.D., P&J Carson Consulting LLC, Ohio, es vicepresidenta del comité de calidad y estadística (E11).

John Carson, Ph.D., de P&J Carson Consulting LLC, Findlay, Ohio, es el coordinador de la columna Puntos de datos. Es presidente del subcomité de control de calidad estadístico (E11.30), miembro del comité de calidad y estadísticas (E11) y miembro de los comités de productos a base de petróleo, combustibles líquidos y lubricantes (D02), calidad del aire (D22) y evaluación ambiental, gestión de riesgos y acción correctiva (E50).