Standardization News:

Q: ¿Cómo se puede estimar la probabilidad de detección (POD) para un tamaño objetivo dado usando datos con dos resultados posibles (hallazgo/sin hallazgo) a partir de un sistema de ensayos no destructivos (nondestructive testing, NDT)?

R: En la industria aeroespacial, un inspector de NDT puede tener que encontrar un defecto tipo fisura de un tamaño crítico dado con al menos 90 % de POD y 95 % de confianza para que un dispositivo cumpla los requisitos de diseño. Para demostrar que la confiabilidad del NDT satisface estos requisitos, se somete a prueba un sistema de inspección para obtener datos que se pueden analizar estadísticamente. Cuando la respuesta de la inspección es “hallazgo” o “sin hallazgo”, es posible obtener una estimación de la POD para un tamaño objetivo dado si el ensayo se diseña como un experimento binomial.

Un experimento binomial consiste de n ensayos de Bernoulli independientes. Un ensayo de Bernoulli es un experimento probabilístico individual que tiene como resultado “éxito” o “fracaso” en el que la probabilidad de éxito tiene un valor p fijo. El problema define qué constituye un éxito y no representa necesariamente un evento deseado. Aunque una fisura de tamaño crítico en el dispositivo es un evento no deseado, por ejemplo, encontrarla con NDT constituye un “éxito”.

El resultado de un ensayo de Bernoulli individual proporciona poca información sobre el proceso subyacente que rige el ensayo. Por ejemplo, el resultado (ya sea hallazgo o sin hallazgo) para un defecto tipo fisura de tamaño crítico no brinda mucha información sobre la POD. Sin embargo, el conjunto de resultados de ensayos de Bernoulli repetidos (por ejemplo, datos hallazgo/sin hallazgo de varios defectos tipo fisura de tamaño crítico) sí lo hace y se describe mediante una distribución binomial con función de probabilidad

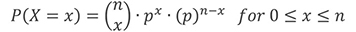
donde P(X = x) es la probabilidad de x éxitos en n ensayos independientes, p es la probabilidad fija de éxito en un ensayo individual y

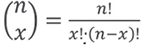
es el número de formas en que x éxitos podrían ocurrir en n ensayos.¹

La suposición de n ensayos independientes con una probabilidad fija de éxitos en un ensayo individual es clave y se puede ilustrar usando un mazo de cartas. Supongamos que la función de probabilidad binomial se utilizará para calcular la probabilidad de sacar un as (un éxito) en cinco ensayos. En este ejemplo, p es conocido porque el número de ases (4) y el número total de cartas en el mazo (52) son conocidos. Sin embargo, el valor de p depende de cómo se realice el experimento. Un experimento binomial requiere que una carta que se extrae del mazo se coloque nuevamente en el mazo y que el mazo se baraje antes de sacar la siguiente carta. Cuando las cartas se extraen con reemplazo sabemos que el valor de p es 4/52 = 0,08 y es el mismo para cada ensayo, manteniendo la independencia de cada ensayo. Si la primera carta que se extrae es un as y no se vuelve a colocar en el mazo, entonces al extraer la segunda carta p es 3/51 = 0,06. La probabilidad de éxito ya no es la misma para la segunda carta que se extrae porque depende de la primera carta que se extrajo. Por lo tanto, diseñar el experimento de forma que los ensayos sean independientes con la misma probabilidad de éxito es clave para suponer un experimento binomial y usar la función de probabilidad binomial.

Leer más: Liderazgo con el alma en la suela: conozca al presidente de ASTM para 2023: Bill Ells

En la aplicación del NDT, donde x es el número de hallazgos exitosos de n oportunidades de inspección independientes, el interés no está en la probabilidad de un resultado dado P(X = x) sino en el de p, que representa la POD para un ensayo individual. A diferencia de un mazo de cartas, p es desconocido. Sin embargo, la Ley de los números grandes establece que x/n proporciona una buena estimación ya que se aproxima a p a medida que n aumenta.² Si un inspector de NDT, por ejemplo, tiene 29 oportunidades de inspección independientes para encontrar un defecto tipo fisura de tamaño objetivo dado y encuentra 28 de 29, entonces una estimación de p = POD en función de los datos de la muestra es 28/29 = 0,97. Pero, ¿qué sucede si el inspector encuentra los 29? Aunque p = 29/29 = 1 es una estimación, no es completamente satisfactoria ya que, en realidad, la inspección no puede ser perfecta.

inferior unilateralDado que siempre hay variación presente y nunca se puede eliminar completamente, se establece un límite de confianza en torno a una estimación en función de una única muestra de datos para tomar en cuenta la incertidumbre debida al muestreo. Al cuantificar la POD para un tamaño objetivo dado, se calcula un límite de confianza inferior unilateral para p de forma de estimar la POD mínima con 95 % de confianza usando el Método de Clopper-Pearson, o “Método conservador”, que supone un experimento binomial.³ Cuando hay 29 éxitos de un total de 29 ensayos independientes, el Método de Clopper-Pearson tiene como resultado una estimación de la POD mínima de 90 % con 95 % de confianza. Esta es la base del método de estimación puntual (point estimate method, PEM).

El PEM es un método que se utiliza para calificar a los inspectores de NDT en la industria aeroespacial para realizar una inspección de hallazgo/sin hallazgo para defectos tipo fisura en dispositivos que necesita una POD mínima del 90 % con 95 % de confianza para que un tamaño objetivo dado satisfaga los requisitos de diseño.⁴

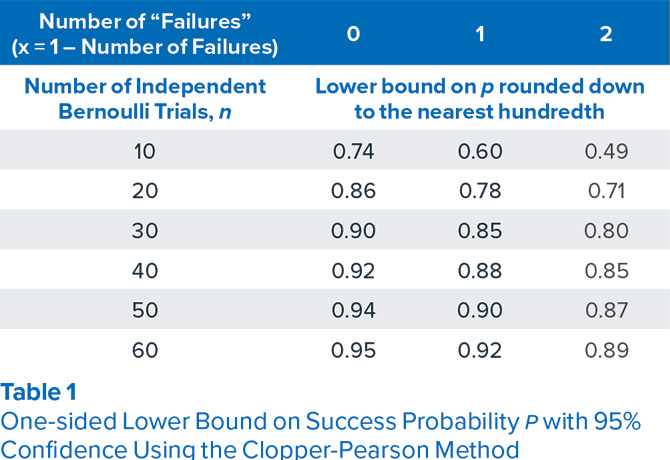
La prueba de calificación del PEM da al inspector 29 oportunidades de inspección independientes de encontrar un defecto tipo fisura de un tamaño objetivo dado. Si se encuentran 29, el requisito de diseño se satisface. Si uno no se encuentra, es posible dar al inspector 17 oportunidades de inspección independientes adicionales. Si se encuentran las 17, lo que tiene como resultado 45 hallazgos totales de 46 oportunidades independientes en total, entonces, con base en el Método Clopper-Pearson se puede afirmar que la POD mínima es del 90 % con 95 % de confianza para el tamaño objetivo dado. (La Tabla 1 proporciona una estimación del límite inferior de p con 95 % de confianza para otros valores de n).

A pesar de que la calificación de un inspector de NDT usando el método PEM es sencilla en términos prácticos, el diseño de la prueba debe satisfacer la suposición de experimento binomial. Dado que la POD no es la misma para tipos de defectos distintos y se espera que aumente con el tamaño para un tipo de defecto dado, los 29 ensayos de Bernoulli deben representar 29 oportunidades de inspección independientes que sean representativas del mismo tipo y tamaño de defecto para que p = POD satisfaga la condición de ser un valor fijo en un ensayo individual. De lo contrario, la integridad estadística de la afirmación de la POD para un tamaño objetivo dado que supone un experimento binomial puede verse comprometida.

Referencias
¹ Dunham, W. The Mathematical Universe: An Alphabetic Journey Through the Great Proofs, Problems, and Personalities. New York: John Wiley & Sons, 1994: 11-22.
² Ibid.
³ Meeker, W.Q., Hahn, G. J., and Escobar, L.A. Statistical Intervals: A Guide for Practitioners and Researchers. Second Edition. New York: John Wiley & Sons, Inc., 2017: 103-104.
⁴ NASA Technical Standards System. “Nondestructive Evaluation Requirements for Fracture-Critical Metallic Components” (NASA-STD-5009).

Descargue este artículo en formato .pdf aquí.