Standardization News:

P. ¿Qué confianza puedo tener en que (llene el espacio en blanco)?

R. Con suficiente investigación, un buen diseño y un proceso controlado, puedo estar bastante seguro. Pero esta no es una pregunta estadística. El término confianza estadística generalmente aparece con los resultados de un análisis estadístico destinado a inferir algo sobre una población o un proceso en función de una sola muestra de datos (que suele llamarse inferencia estadística), donde se supone que la muestra es una representación aleatoria de una población o un proceso estable. Los intervalos estadísticos y las pruebas de hipótesis son métodos comunes y conocidos que se emplean para la inferencia estadística, cada uno con un enunciado sobre la confianza estadística asociado con los resultados. Sin embargo, los especialistas, con frecuencia, entienden mal el significado de la confianza estadística.

En el diccionario en línea Merriam-Webster, la confianza se define como la “fe o creencia de que uno actuará de manera correcta, apropiada o efectiva”. Cuando se utilizan métodos estadísticos para obtener conclusiones sobre la base de los datos de una muestra, nuestra confianza radica en los métodos estadísticos que actúan “de manera correcta, apropiada o efectiva” de modo que las conclusiones alcanzadas sean correctas. La confianza estadística se representa típicamente como un porcentaje con notación , donde  representa un enunciado de probabilidad a largo plazo sobre el método estadístico en sí. Además, la confianza se refiere a un resultado a largo plazo. Es decir, la confianza se refiere a la probabilidad de obtener la conclusión correcta sobre una población o un proceso si el método utilizado se repitiera muchas veces en condiciones idénticas, mediante el uso de diferentes conjuntos de datos de muestra. Los valores comunes para α son 0.01, 0.05 y 0.10, lo que resulta en niveles de confianza iguales a 99 %, 95 % y 90 %, respectivamente. Por ejemplo, un 95 % de confianza significa que la probabilidad de que el método estadístico haya captado correctamente la verdad es del 95 %. El riesgo supuesto de llegar a una conclusión incorrecta se representa con α. Dado un nivel de confianza del 95 %, existe un riesgo de 5 % de que el método estadístico no capte la verdad y se obtenga una conclusión incorrecta.

PARA USTED: Revisión de intervalos estadísticos: intervalos estadísticos comunes, selección de intervalos y ejemplo

En la última entrega de Data Points (vinculado arriba), mostramos cómo se pueden usar los intervalos estadísticos para explicar la incertidumbre en una estimación puntual sobre la base de una sola muestra de datos y con un nivel determinado de confianza estadística.¹ Para ilustrar el significado de la confianza estadística, considere el ejemplo del intervalo estadístico de estimar la proporción verdadera de grageas M&M de color naranja en una bolsa individual. Cuando ocurren x observaciones de interés en una muestra de tamaño n, la proporción de la población se puede estimar como .² Dada una bolsa individual de M&M, la proporción de grageas M&M de color naranja se puede estimar al dividir la cantidad de grageas M&M de color naranja entre la cantidad total de grageas de la bolsa. Pero, ¿qué sucedería si los datos se recopilaron de otra bolsa (es decir, de otra muestra)? ¿La cantidad de grageas M&M naranjas será la misma que en la primera bolsa? ¿La cantidad total de grageas en la bolsa será la misma? Aunque no suele hacerse en la práctica, si tuviéramos que muestrear varias veces, bajo las mismas condiciones, las proporciones de la muestra resultante serían diferentes, ya que los datos recopilados de cada muestra (es decir, de cada bolsa) serían diferentes. Esto ejemplifica la variación debida al muestreo. Además, pueden intervenir otras fuentes de incertidumbre, como la variación inherente en el proceso de fabricación de M&M. Para tener en cuenta esta variación, se puede utilizar un intervalo de confianza para una proporción de población, p, que se calcula como:

, donde  es el punto porcentual superior del 100%•(1-α/2) de la distribución normal estándar, de modo que  y suponiendo  y  son ambos al menos 5._³

Como experimento, 21 especialistas recopilaron de forma independiente los datos reales de una bolsa individual de M&M. A cada investigador, se le dio una bolsa de M&M y se le dijo que estimara la proporción de grageas M&M de color naranja en función de lo que había en su bolsa (es decir, su muestra independiente y aleatoria de la población de M&M). En la Tabla 1, se muestran los datos recopilados por cada investigador junto con la proporción calculada de grageas M&M de color naranja y el intervalo de confianza de 95 % (  en este caso).

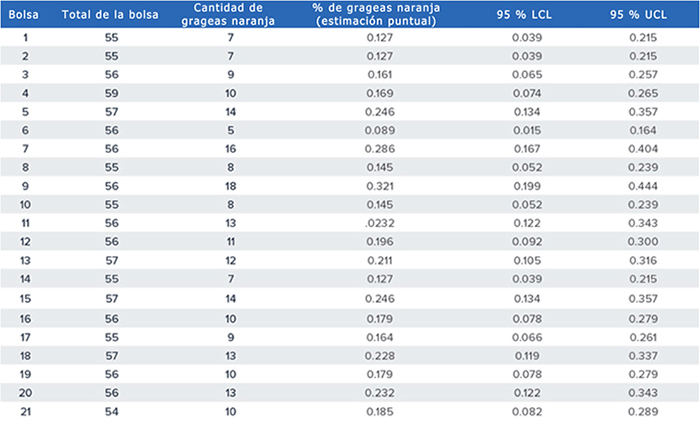
Tabla 1. Resultados de una muestra única de datos recopilados de forma independiente por 21 investigadores, donde LCL y UCL son los límites inferior y superior de confianza, respectivamente, para un intervalo de confianza de 95 % bilateral de una proporción de población.

Considere al investigador que tenía la bolsa 1. Según los resultados, el investigador calcula que la proporción verdadera de grageas M&M de color naranja en una bolsa está entre 3.9 % y 21.5 % con 95 % de confianza. En el contexto de intervalos estadísticos, una confianza de 95 % se refiere a la probabilidad de que el intervalo haya captado correctamente la verdad, lo que significa que existe un riesgo de 5 % de que el intervalo estadístico no haya captado la verdad y se llegue a una conclusión incorrecta.

En la Figura 1, se presenta el intervalo de confianza calculado por cada investigador junto con la proporción verdadera de M&M, que era de 20 % cuando se recopilaron los datos de la Tabla 1.

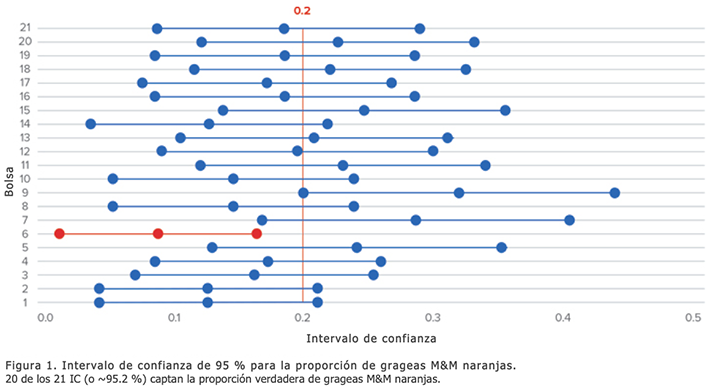
Tenga en cuenta que el intervalo estadístico calculado por el investigador que tenía la bolsa 1 incluye el 20 %. El método de intervalo estadístico utilizado en este caso captó correctamente la verdad y se obtiene una conclusión correcta, es decir, la verdadera proporción de grageas naranja se ubica de hecho entre 3.9 % y 21.5 %. Para el investigador que tenía la bolsa 6, el método de intervalo estadístico no captó la verdad y la conclusión obtenida es una subestimación de la proporción verdadera. Pero la probabilidad de alcanzar una conclusión incorrecta es de aproximadamente 5 %, como lo ilustra el hecho de que 1 de los 21 intervalos estadísticos o aproximadamente el 4.76 %, no logró captar la proporción verdadera de las grageas naranjas. Esto explica que, en un único experimento, se tiene 95 % de confianza de que se obtendrán las conclusiones correctas sobre la población o el proceso sobre la base de la inferencia estadística realizada a partir de una única muestra de datos.

En resumen, la confianza estadística es una declaración de probabilidad sobre la efectividad a largo plazo del método estadístico para alcanzar una conclusión correcta. Entonces, ¿qué tan seguros podemos estar de tener un 20 % de grageas M&M naranja en nuestra bolsa? Pregunte a la división de confitería Mars Wrigley de Mars, Incorporated, no a un estadístico. ■

Referencias

1. Luko, S. and Brown, J. “Revisiting Statistical Intervals.” Standardization News (Jan./Feb. 2024): 48-50.
2. Luko, S. and Neubauer, D.V. “Statistical Intervals Part 1: The Confidence Interval.” Standardization News (julio/agosto 2011): 18-20.
3. Ibid.

Información sobre el autor

Stephen Luko es un estadístico jubilado con 40 años de experiencia en la industria, con el título de miembro en Collins Aerospace, ASTM International y la American Society for Quality. Actualmente, preside el subcomité de confiabilidad (E11.40) y fue presidente del comité de calidad y estadística (E11).

Jennifer Brown es estadística y tiene 16 años de experiencia en la industria aeroespacial. Preside el subcomité de terminología (E11.70) y es miembro del subcomité de métodos especializados de ensayos no destructivos (E07.10).

El dr. John Carson es estadístico sénior de Neptune and Co. y coordinador de la columna Data Points. Es miembro de los comités de calidad y estadística (E11), productos derivados del petróleo, combustibles líquidos y lubricantes (D02), calidad del aire (D22) y otros.